Osiem set
Drugie zadanie z poprzedniego wpisu jest potwierdzeniem tego, że ułożenie łamigłówki z setkami tak, aby miała dokładnie jedno rozwiązanie, to nie przelewki. Sprokurowałem je, zmieniając tylko jedną cyfrę w pierwszym zadaniu, bo z tak utworzonym dziełkiem łatwo sobie poradzić – wystarczy zauważyć, że po dopisaniu 4 do 9 w prawym górnym rogu, czyli po utworzeniu liczby 94, cztery liczby w diagramie pozostają jednocyfrowe i uzupełnienie cyfr w czterech pozostałych polach jest już bardzo proste. Niestety, dokonując zmiany pominąłem obecność innych rozwiązań, których – jak się okazało – jest w sumie aż osiem. To dowód, że przy rzetelnym układaniu „setek” praktycznie przydaje się albo nawet jest niezbędne wsparcie komputerowe.
Teoretyczną podstawą zadania są partycje, a konkretnie podziały liczby 100 na trzy części – od (1, 1, 98) do (33, 33, 34). Są 884 takie podziały. Zadanie, a ściślej jego rozwiązanie, jest minikrzyżówką z sześciu partycji. Ile różnych takich krzyżówek oraz ile różnych zadań 3×3 można ułożyć – nie wiem. Problem obliczeniowy wydaje się bardzo trudny. Jeszcze trudniej jest dla podziałów 100 na cztery części – od (1, 1, 1, 97) do (25, 25, 25, 25) – których mamy 7153. Odpowiednia krzyżówka jest wówczas kwadratem 4×4. Czy trudniej ją rozwiązać niż 3×3? Proszę spróbować.
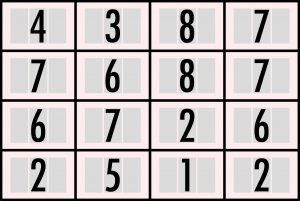
Przypominam: część 16 cyfr, a na pewno większość, należy uzupełnić sąsiadką, dopisując obok (przed lub za) odpowiednią cyfrę. Po dopisaniu w kratce powstaje liczba dwucyfrowa. Cały ten zabieg należy przeprowadzić tak, aby suma czterech liczb w każdym z czterech wierszy i w każdej z czterech kolumn diagramu była równa 100.
Czy rozwiązanie jest jedno. Powinno tak być, ale głowy nie dam.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Zadanie ma jedno rozwiązanie:
{{4 13 8 75} {7 6 80 7} {65 27 2 6} {24 54 10 12}}
AI mówi, że jest więcej niż jedno rozwiązanie.
No i widać jak z tym AI jest – dużo szumu , a jak się odrobinę głębiej zanurzyć, to okazuje się, że jest jedno rozwiązanie.
4+13+8+75
7+6+80+7
65+27+2+6
24+54+10+12
ergo:
AI jest bardzo przereklamowane.
AI AI nie równa:)
mp
Różnych krzyżówek 3×3, w których sumy wierszy i kolumn wynoszą 100, jest aż 11 768 526 (tę liczbę trzeba by okroić wykluczając obroty i odbicia).
Ale dla ilu z nich można by ułożyć fajne zadanie – czyli takie z jednym rozwiązaniem – tego nie wiem i w sumie nawet nie mam pomysłu, jak by to można było szybko sprawdzić (o ile w ogóle się da).
Losowo wybrałem taką macierz spośród powyższych 11,8 mln propozycji:
Następnie znów losowo wybrałem cyfry do hipotetycznego zadania, którego jednym z rozwiązań byłaby macierz powyżej:
No i okazało się, że dla takiego zestawu jest aż 20 odpowiedzi.
Ciekawe. Czy jedynym sposobem na szukanie układów z jednym rozwiązaniem jest metoda prób i błędów, czyli losowe wybieranie i sprawdzanie, ile jest rozwiązań?
mp
W poszukiwaniach układów z jednym rozwiązaniem z pewnością przyda się następująca obserwacja:
W aktualnym zadaniu 4×4 drugi wiersz może składać się z jednego z sześciu zestawów dających sumę 100.
Natomiast wiersz czwarty ma takich możliwości ponad siedemset.
(Drugi wiersz ma cyfry duże, natomiast czwarty raczej małe.)
Generalnie:
Ilość rozwiązań jest uzależniona od tych ilości potencjalnych zestawów dla poszczególnych wierszy/ kolumn.
Im większa suma ujawnionych cyfr, tym mniejsza oczekiwana ilość rozwiązań.
Dzięki. To jakby poszlaki, ale zawsze coś.
mp
PRYWATNIE:
(proszę usunąć po przeczytaniu):
Z ciekawości odrobiłem zadanie z tematu generowania zadań z jednym rozwiązaniem i rozmiar 3×3 nie stanowi problemu.
Zadań 4×4 nie próbowałem, ale pewnie się jeszcze pochylę.
Rozumiem, że generowanie metodą siłową.
(Usunę później, być może hurtem:)
mp
Spostrzeżenie apartado jest bardzo ciekawe – oznaczałoby, że poszukiwania warto by zacząć od zestawów złożonych z dużych ujawnionych cyfr.
Ja przez ostatnią dobę niczego odkrywczego nie wymyśliłem, ale nie sądzę, aby losowe wybieranie i sprawdzanie, ile jest rozwiązań, było najlepszą strategią.
Wspomagając się komputerem, można by wyjść od zestawów, a nie od macierzy dających sumę 100 w wierszach i kolumnach. Czyli dla macierzy 3×3 mamy 9^9 możliwych zestawów, a dla macierzy 4×4 mamy 9^16 możliwych zestawów (minus odbicia i obroty). Idąc od tyłu, czyli od zestawów składających się z samych dziewiątek, można by pewnie dość szybko znaleźć takie, dla których jest tylko jedno rozwiązanie.
Ale nadal jest to droga bruteforce’owa, a więc pozbawiona jakichkolwiek znamion elegancji. Przydałby się jakiś magic bullet od genialnego matematyka, który znalazłby sposób, aby przyspieszyć poszukiwania:)
Wracając do głównego wątku, widzę jedno rozwiązanie:
Szanowny Panie Marku
Bardzo proszę o usunięcie ostatniego wpisu z 20 lutego 2023 1:50 sygnowanego moim nickiem xswedc. Pochodzi on z mojego konta, lecz nie jest moim dziełem.
W skrócie: w towarzystwie paru znajomych męczyliśmy przez kilka godzin nową atrakcję internetu chatGPT różnymi zadaniami, w tym wieloma z Łamibloga. Było ciekawie, lecz było przy tym wino i jedna osoba niezbyt dobrze je tolerująca. Wysłana wiadomość jest skutkiem splotu tych wydarzeń oraz tego, że nie dopilnowałem komputera.
Bardzo przepraszam i pozdrawiam
Waldemar Zieliński
ps1 Autor żenującej wiadomości chciałby przeprosić osobę o niku ersonasolidna, nie wie jednak jak to zrobić.
ps2 Nie mogłem wysłać tej wiadomości pocztą, gdyż po niedawnych zmianach w sprzęcie i oprogramowaniu straciłem książkę adresową. Proszę więc tego również nie publikować. Tyle zamieszania, jeszcze raz przepraszam…
Usunąłem. Ten usunę później hurtem przy uwalnianiu komentarzy.
mp
@xswedc
Jak długo liczy program napisany przez chatGPT, bo mój ok. trzy sekundy
@Spytko
Ja czasami używam chatGPT, ale w tym zadaniu akurat mi nie pomógł. To jednak kwestia ułożenia odpowiedniego promptu, kwestia prób i błędów.
Natomiast mój skrypt wyszukuje rozwiązanie 4×4 w 0.5 sekundy (rozwiązanie 3×3 znajduje w 0.03 sekundy), jednak wiele zależy od komputera. Ja mam kilkuletniego laptopa, który w momencie produkcji był dość dobrej klasy. To prosty skrypt jest w pythonie, a to przecież nie jest specjalnie szybki język (przy czym w pewnych zastosowaniach, jeśli użyje się bibliotek takich jak numpy czy scipy, python potrafi być niesamowicie szybki, ale to temat na inną rozmowę).
Wrzuciłem ten skrypt na githuba, ale nie wiem, czy publikacja permalinku nie byłaby złamaniem zasad (jest to trochę jak opublikowanie wyniku). Ewentualnie opublikuję w piątek wieczorem.
Te czasy to nadal za dużo, aby znaleźć populację wszystkich zagadek z jedynym rozwiązaniem. Ale jestem w stanie wyciągnąć dużą próbkę zagadek, np. wylosować 100 000 zestawów 3×3 albo 10 000 zestawów 4×4 i spośród nich wskazać, które mają jedno rozwiązanie. Na podstawie tej próbki można też wnioskować, czy są jakieś poszlaki, czy zestawy z jednym rozwiązaniem mają jakieś wspólne cechy, np. jak sugerował apartado – czy mają wiersze lub kolumny z relatywnie dużymi wartościami.
Jak dojdę do jakichś ciekawych wniosków, to się tutaj podzielę:)
Link do skryptu na github (odrębnie, bo nie wiem, czy można):
https://github.com/ersonasolidna/lamiblogswiatnauki/blob/83a901e3267fa82f3c8d5d66779689f7ccbca49b/2023-02-18_Lamiblog_Osiem_set.py
wyszło mi tylko jedno rozwiązanie:
tak jak apartado zauważył im większe cyfry tym mniej rozwiązań, poza czwartym wersem ilość możliwych setek jest w granicach rozsądku (45-83), co w połączeniu z 6 kombinacjami z drugiego wersu daje możliwość wyeliminowania niepasujących kombinacji.
Rozwiązanie jest jedno:
Dobry wieczór,
Uff – jest:
4 13 8 75
7 6 80 7
65 27 2 6
24 54 10 12
Pozdrawiam
Niestety nie udało mi się wywnioskować niczego ciekawego o zagadkach 4×4, ale ze statystyk dla zagadek 3×3 płyną następujące wnioski.
Udział zagadek 3×3, które mają rozwiązanie, systematycznie maleje wraz ze wzrostem sumy cyfr macierzy 3×3. Jednak udział zagadek, które mają tylko 1 rozwiązanie, zachowuje się odwrotnie – rośnie wraz ze wzrostem sumy cyfr. Dla sum między 47 a 51 aż 50-60% rozwiązań to rozwiązania unikalne.
Dla wysokich sum są fluktuacje, np. dla sumy cyfr=65 jest 14% szansy, że trafimy na zagadkę, która ma rozwiązanie, ale już 76% tych rozwiązań jest unikalnych, a dla sumy 68 liczby te wynoszą odpowiednio 20% i 55%. Jednak zadania z tak wysoką sumą jak 65 są bardzo nudne, bo występują tam np. niemal same ósemki (tak samo jak dla niskich sum panoszą się jedynki).
ersonasolidna.pl/lamiblog/20230218_Osiemset/Wykres3n3.png
Na powyższej ilustracji znajduje się przybliżony wykres obrazujący oba zjawiska: 1) czy jest zadanie z rozwiązaniem 2) czy to rozwiązanie jest jedyne (unikalne). Dziwne „uskoki” dla sum cyfr powyżej 53 wynikają ze sposobu doboru próby – są to po prostu losowe błędy wynikające z małej próby, natomiast dla sum cyfr 65 i 68 na prawnym skraju są to dane dla populacji, a więc liczby poprawne.
Zadanie z poprzedniego odcinka:
Miało sumę cyfr 41, przy której było 35% szansy, że jest to rozwiązanie unikalne.
Natomiast to samo zadanie z wymienioną ósemką na czwórkę miało sumę cyfr 37, a w takim przypadku jest już tylko 17% szansy, że jest jedno rozwiązanie. I rzeczywiście zadanie tamto miało 8 rozwiązań.
Przykładowe zadanie z jednym rozwiązaniem o sumie cyfr 48 wygląda tak:
Zadania o sumie cyfr 48 mają 55% szansy, że mają jedno rozwiązanie.
Szukałem odpowiedzi na pytanie: czy wysoka suma cyfr w pojedynczej kolumnie lub pojedynczym wierszu jakoś zwiększa prawdopodobieństwo, że zadanie ma jedno rozwiązanie – niczego takiego nie udało się potwierdzić. Tak naprawdę nie zauważyłem żadnej godnej uwagi reguły, która mogłaby ułatwić układanie zadań.
Co do macierzy 4×4, to nie wiem, czy występują analogiczne wzorce. Jedyne, co zauważyłem na 2 bardzo małych losowych próbach, to że każda z nich zwróciła zupełnie inne wyniki i tylko utwierdziłem się w przekonaniu, że nie można wnioskować na podstawie małej próby:)
Kilka zadań 4×4 z jednym rozwiązaniem: ersonasolidna.pl/lamiblog/20230218_Osiemset/przykladyzadan4n4.txt
@ ersonasolidna
Dzięki za wykres – właśnie tak to sobie wyobrażałem wspomagany intuicją.
@ ersonasolidna
Odnosząc się do tych słów:
”
Dla sum między 47 a 51 aż 50-60% rozwiązań to rozwiązania unikalne.
”
Podoba mi się, że to maksimum wypada bardzo blisko wartości 0.618 x 81.
81 to maksymalna suma dla macierzy 3×3, a 0.618 omówione jest tu:
https://en.wikipedia.org/wiki/Golden_ratio
@ apartado
To faktycznie ciekawa zbieżność, ale podejrzewam, że dla populacji (a nie próby) były inne wyniki:)
@xswedc
Tak podejrzewałem, że to jakaś imprezowa sytuacja, więc absolutnie się nie gniewam:) Korzystając z możliwości wygłoszenia laudacji na cześć zakrapianych imprez wokół łamibloga, Świata Nauki i innych zagadek, chciałem powiedzieć, że w naszym kilkuosobowym gronie też czasem ścigamy się na rozwiązywanie łamigłówek albo omawiamy sposoby rozwiązań. Często trwa wyścig z czasem w piątkowe popołudnie, gdy już czas zacząć imprezę, ale jeszcze trzeba zdążyć wysłać rozwiązanie zanim się ujawni. Szczególną sympatią darzę jednak wspomnienia związane z rozwiązywaniem zagadek szachowych, co zwykle ma jednak miejsce w domowym zaciszu i na osobności („dobra, daję sobie 10 minut i idę spać, bo już późno” – po czym mija godzina, jak w przypadku zadania 2 z listopadowego numeru ŚN, w który trzeba było określić pierwszy ruch białych). Mają one w sobie coś magicznego, bo zamiast kartki papieru i ołówka (a w zasadzie już dziś głównie tableta i pencila) trzeba otworzyć to drewniane pudło, wyłożyć figury i trochę pogłówkować. I potem porozmawiać, w jaki sposób każde z nas doszło (albo i nie) do rozwiązania.