Miodowo krytycznie
„Zębaty” sześciokąt foremny złożony z 61 małych sześciokątów jest miejscem akcji Wysp miodowych – łamigłówki wymyślonej w roku 1999 przez węgierskiego matematyka i psychologa László Merő. Ściśle rzecz biorąc, chodzi o podstawową wersję tej łamigłówki, bo bywają odmiany, różniące się od oryginału niektórymi parametrami. Łamigłówka nie jest zbyt popularna, bowiem jej rozwiązywanie jest zwykle mocno zagadkowe, a logiczne nie za bardzo, choć próbowanie i błądzenie ma w tym przypadku sporo uroku. W Łamiblogu Wyspy gościły już niespełna 12 lat temu, więc tylko zwięźle przypomnę instrukcję obsługi.
Niektóre pola diagramu są zaszarzone, a trzeba zaszarzyć jeszcze kilka lub kilkanaście następnych tak, aby pozostałe utworzyły sześć odrębnych wysp – każda powinna składać się z sześciu jasnych pól. Rzec by można, celem jest pojawienie się piaszczystego archipelagu – jak w poniższym przykładzie.
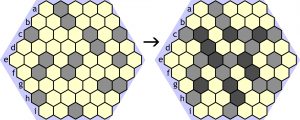
Powracam do Wysp, bo jeden z najaktywniejszych tutejszych komentatorów Antyp1958, zaskoczył mnie informacją, dotyczącą związanego z tą łamigłówką tzw. podzbioru krytycznego. Chodzi o najmniejszą część danego zbioru, której znajomość umożliwia przy określonych warunkach odtworzenie pełnego zbioru. Żaden podzbiór mniejszy od krytycznego nie wystarcza do rekonstrukcji całości. Na przykład w przypadku sudoku podzbiór krytyczny stanowi 17 cyfr umieszczonych na początku w diagramie. Inaczej mówiąc, ujawnienie na starcie 17 odpowiednio rozmieszczonych cyfr teoretycznie wystarcza, aby rozwiązać zadanie, czyli wpisać 64 pozostałe. „Teoretycznie”, bo w praktyce większość takich zadań sudoku jest diabelnie trudna, właściwie nie do rozgryzienia bez komputerowego wsparcia.
W Wyspach miodowych do zaszarzenia jest 61-36=25 pól. Ile z nich tworzy podzbiór krytyczny, czyli ile co najmniej trzeba ujawnić na początku, by prowadziły do unikalnego rozwiązania? W przypadku sudoku podzbiór krytyczny stanowi 17/81=21% pełnego zbioru. Gdyby zachować tę proporcję, to w Wyspach należałoby zaszarzać na początku nie mniej niż 5 pól, a ściślej 5 i ćwierć. Antyp1958 postanowił to sprawdzić, pisząc odpowiedni program. Rezultat potwierdził przewidywania, ale patrząc na poniższy przykład zadania z ujawnionymi pięcioma szarymi polami trudno uwierzyć, że rozwiązanie jest tylko jedno, czyli jest tylko jeden sposób zaszarzenia jeszcze 20 pól tak, aby pozostało sześć 6-polowych wysp.
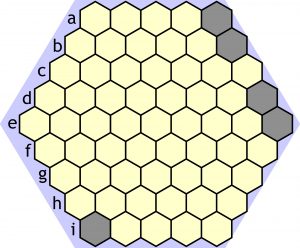
Rozwiązanie tego zadania na piechotę wydaje się prawie niemożliwe, ale gdyby komuś się udało, to proszę o podanie współrzędnych 20 zaszarzonych pól, korzystając z liter przy brzegu diagramu (wstępnie zaszarzone pola – a5, b6, d8, e9, i1). Przynajmniej równie cenne będą uwagi dotyczące sposobu rozwiązywania.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Rozwiązanie:
https://images92.fotosik.pl/570/9857437dfacf9148.jpg
Sposób rozwiązania:
Po kilkudziesięciu próbach i poczynionych obserwacjach wywnioskowałem, że:
1. pole h2 musi być szare
2. jedno z pól c6, d7 musi być szare
3.1. jeżeli obie początkowe grupy szarych pól (a5, b6) oraz (d8, e9) są połączone z resztą szarych pól to na planszy nie może być trójki wzajemnie sąsiadujących szarych pól (np.: (f3, g2, g3) albo (a5, b5, b6):
o o olub
3.2. jeżeli jedna z grup (a5, b6) lub (d8, e9) sąsiaduje wyłącznie z białymi polami, to na planszy musi wystąpić dokładnie jedna trójka wzajemnie sąsiadujących szarych pól.
4. za wyjątkiem opisanej ew. trójki wzajemnie sąsiadujących szarych pól wszystkie pozostałe rozgałęzienia muszą być utworzone z czterech pól:
o o o o lub o o o oTeraz to już łatwo, gdyż wystarczy sprawdzić dosłownie kilka wariantów wychodzących z narożnika i1 i ich kilka podwariantów:
wariant 1 o o o o o o i1 -> o wariant 2 o o o o o o o i1 -> o wariant 3 o o o o o o o i1 -> oOkazało się, że wariant 2 w zasadzie sam się rozwiązuje:
https://images92.fotosik.pl/570/cc6ee9ebf70ca86e.jpg
Na rys. 1 jest on w jasnym szarym kolorze. Zielone pole to jednoznaczne zamknięcie obszaru z 6 białych pól.
Na rys. 2 widać domknięcie kolejnego obszaru. Można to zrobić inaczej, ale z zaszarzeniem pola c7, co jest bez sensu.
Na rys. 3 dwa kolejne kroki. Najpierw zielone pola, a następnie z niebieskimi nie ma już problemu. Na ostatnim rysunku widać inny „zielony” wariant i po nim brak rozwiązania.
@mp
„W Łamiblogu Wyspy gościły już niespełna 12 lat temu”…
Wielce Szanowny Panie Marku.
W dawnych dobrych czasach gdzieś na dole strony wyszukałbym link do tego zadania i cośtamtego, albo też i nie. A teraz co, paski w tvp info mam czytać? Brrr…
Proszę ratować mnie (nas) przed zgubą i oddać linki do starych zadań. Toż to historia, dziedzictwo, kultura itd… Nie można przecież tego ot tak, po prostu na śmietnik! Aż ciśnie się na usta hymn łamiblogowiczów:
谜题–永恒的青春,嗬嗬嗬!
https://penszko.blog.polityka.pl/2010/07/15/po-wegiersku/
Od czasu do czasu odwiedzam ten blog i jeżeli jakieś zadanie spodoba mi się, biorę się za nie. A jak już się wezmę, to nie odpuszczę, póki go nie pokonam. Z rozwiązaniami już się nie chwalę, odstręcza mnie pisanie.
I tak było z ostatnim zadaniem. Ale gdy mnie zainteresowało, jak uczestnicy blogu podeszli do zadania i zobaczyłam tylko jeden wpis z rozwiązaniem, postanowiłam podzielić się moim rozumowaniem.
Do rozwiązania, tego samego co xswedc, doszłam i ja, ale pozwolę sobie przedstawić sposób, w jaki tego dokonałam. Wpierw upierałam się, że wszystkie wyspy muszą koniecznie przylegać do brzegu (skąd ten upór, nie wiem). Po kilku nieudanych próbach zadałam sobie pytanie: a może jedna wyspa nie przylega do brzegu? Jeżeli tak, to potrzeba co najmniej 12 szarych pól na otoczenie tej wyspy i wtedy pozostaje najwyżej 8 pól na oddzielenie od siebie pozostałych 5-ciu wysp. Są dwie możliwości oddzielenia ich szarymi polami: 1,1,2,2,2 lub 1,1,1,2,3. Wyspa zatem musi być bardzo obła, by znalazła się możliwie blisko brzegu. Dla trzech rodzajów wysp wystarczy 12 pól: „trójkąt”, „równoległobok” i „nerka”. Pierwsze dwa odpadały (trójkąta jeden wierzchołek miał za daleko do brzegu, równoległoboku obydwa dłuższe boki też), pozostała nerka. Trochę nią pokręciłam, by znaleźć właściwe ułożenie. Sposobem oddzielenia okazała się możliwość 1,1,2,2,2. I już!
Pozdrawiam wszystkich blogowiczów.