Sudomino
Wpadło mi w oko jeszcze jedno małe i mocno nietypowe parasudoku, więc zanim wypadnie postanowiłem je wyświetlić w Łamiblogu. Zwłaszcza że kojarzy się z dominem, do którego mam słabość.
Prostokąt 8×8 z otworami ułożony jest jakby z 28 kamieni domina (1×2), a ściślej – nie ze zwykłego kompletu, lecz wyłącznie z kamieni zwanych dubletami. Przypomnę, że dublet to kamień, na połówkach którego są takie same liczby oczek. Aby nie komplikować rysunku, na diagramie na kamieniach oznaczono po jednej cyfrze wspólnej dla dwu połówek.
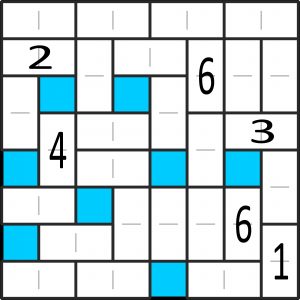
Zadanie polega na wpisaniu cyfr od 1 do 6 na pozostałych kamieniach tak, aby w żadnym z ośmiu wierszy, ani w żadnej z ośmiu kolumn cyfry się nie powtarzały. Oczywiście, jeśli cały dublet leży w jednym rzędzie, to na jego połówkach są dwie jednakowe cyfry, ale – zgodnie z przyjętą konwencją – taki dublet cyfr jednoczymy, tzn. uważamy go za jedną cyfrę, obsługującą obie połówki (jak na diagramie).
Jak wynika z układu kamieni, liczba cyfr w rzędach nie będzie taka sama. Wprawdzie w większości rzędów znajdzie się ich sześć, ale w niektórych cztery lub pięć.
W rozwiązaniu wystarczy podać siedem kolejnych cyfr na kamieniach leżących na przekątnej łączącej lewy dolny róg z prawym górnym.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
3522612
3,5,2,2,6,1,2
Mocno relaksujące.
3522612
3, 5, 2, 2, 6, 1, 2
Wydało się – z tym dominem to ściema – puścił Pan oczko.
? (mp)
21 – szybko poszło 😀
// co do sudokopodobnych to ciekawe są sudoku wiązane – ten sam układ liczb w dwóch diagramach, inne reguły.
W kolejności od lewego dolnego do prawego górnego rogu : 3 5 2 2 6 1 2
3,5,2,2,6,1,2
Od góry rzędami
6132
235614
5x3x2614
546213
x42x1x5
1×34265
x534261
34×51
Trzy pięć dwa, dwa sześć, dwanaście – efekt domina, motyla czy mrówki?
Gdy zobaczyłam rozwiązanie p. Xswedc-a, pomyślałam, że wynik to pewnie 21 . I rzeczywiście, suma liczb na podanej przekątnej tyle właśnie wynosi.
Też zauważyłem,ale uwolniłem od razu, bo to tylko mały kluczyk do rozwiązania.
mp
W_sumie muszę się zgodzić z xswedc. Oczko.
Z xswedc trudno się nie zgodzić.
mp
3,5,2,2,6,1,2