Daję czadu

18 lipca 2017
Marek Penszko

Dwunasty Omnibus ruszył w trasę miesiąc temu, a ja otrzymałem zamówienie na trzynasty. Zacząłem więc główkować nad zadaniami, a jedno z nich postanowiłem zaprezentować tu i teraz jako zajawkę tego, co oficjalnie zadebiutuje – jeśli wszystko dobrze pójdzie – za mniej więcej pięć miesięcy. Pomysł zadania nie jest mój; przyznaję się tylko do „czadowej” formy oraz pewnego drobiazgu, ale o tym za chwilę.

Czad jest związkiem węgla i tlenu. Wzór chemiczny jego cząsteczki składa się z symboli tych pierwiastków – jednego C i jednego O. W diagramie jest 14 cząsteczek (w przykładzie 8), ale ujawnione są tylko wchodzące w ich skład błękitne atomy tlenu. Zadanie polega na uzupełnieniu braków, a więc wpisaniu w niektóre puste kratki symboli C. Każde C powinno pojawić się obok O (w tym samym wierszu lub kolumnie) uzupełnione wiązaniem, czyli kreską łączącą obie litery. Żadne dwa symbole C nie mogą znaleźć się w sąsiednich polach, także stykających się tylko rogiem.

Przykład:

Zadanie:

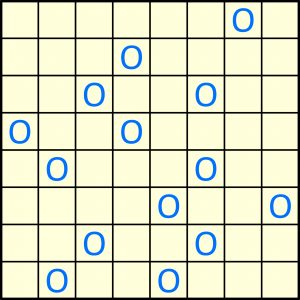
W oryginalnej wersji tego rodzaju zadania, wymyślonej i opublikowanej po raz pierwszy przed blisko 30 laty w Holandii, zamiast cząsteczek CO są namioty przywiązywane do drzew. Jest też drobna różnica merytoryczna: przed wierszami i nad kolumnami – wszystkimi lub tylko niektórymi – umieszczone są liczby; każda określa, ile namiotów powinno pojawić się w danym wierszu (kolumnie). Zauważyłem jednak, że możliwe jest małe „ulepszenie”: drzewa, a w wersji chemicznej atomy tlenu, można tak rozmieścić, że liczby obok diagramu nie będą konieczne. Stąd powyższe zadanie. Obawiam się jednak, że w tym przypadku nie sposób dotrzeć do rozwiązania tylko na logikę, czyli wnioskując jak po sznurku; trzeba choć trochę próbować i błądzić. Czy mam rację?
Jeśli w rozwiązaniu „zaszarzyć” pola zajęte przez cząsteczki, to podzielą one diagram na jasne części. W rozwiązaniu wystarczy podać, ile jest tych jasnych części i z ilu pól składa się każda z nich (w przykładzie części są dwie – 2- i 18-kratkowa).