Raz, dwa, trzy
Układamy łamigłówkę małego formatu: w trzech polach diagramu 3×3 należy rozmieścić cyfry 1, 2 i 3 tak, aby łamigłówka miała jedno rozwiązanie. Na ile sposobów można to zrobić, czyli ile różnych łamigłówek można utworzyć (z dokładnością do obrotów i odbić lustrzanych)?
Wypadałoby jeszcze podać, jaka łamigłówka jest na tapecie, czyli wyłożyć, a właściwie przypomnieć jej zasady. Otóż chodzi o macki (https://penszko.blog.polityka.pl/2011/03/11/moc-macek/ – proszę tu zerknąć, gdyby zechcieli Państwo pobawić się w rozwiązywanie układania).
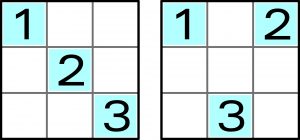
Gwoli jasności poniżej dwa kontrprzykłady: w pierwszym cyfry rozmieszczone są tak, że rozwiązania nie ma, w drugim – rozwiązania są dwa.

Komentarze
Znalazłam 5:
http://pokazywarka.pl/w6qdsu/
To jeszcze nie komplet.
mp
Śpieszę z rozwiązaniem, zanim OlaGM zrobi to swoje tradycyjne makro w Excelu 😉
Obstawiam 18.
Chociaż jak się człowiek śpieszy…
Trochę wolniej: wynik 16.
Czy to i poprzednie rozwiązanie nie dotyczą przypadkiem innego zadania? Szukamy układów cyfr, które mają dokładnie JEDNO rozwiązanie.
mp
7
Na makro w Excelu tym razem nie mam pomysłu 😉 Metodą kartki i ołówka otrzymałam 9 rozwiązań.
Pominąłem, z nieznanych mi przyczyn, dwa rozwiązania. Więc razem 9.
Jeśli i tym razem kropnąłem się, to jeszcze nie wiem co, ale na pewno coś…
Jeszcze coś 🙂
mp
Faktycznie przeoczyłem tę informację o jednym rozwiązaniu.
Pokombinowałem na nowo i właśnie wszedłem na bloga, żeby zamieścić odpowiedź „7”, ale zmieniłem zdanie 😉
Jeszcze się trzeba podelektować myśleniem.
Przy okazji dzięki dla @Markoniusz za poszerzenie horyzontów w zakresie liczb autobiograficznych.
http://pokazywarka.pl/wl61d5/
To wciąż nie jest komplet.
mp
Ostatecznie 10. Teraz to już powinien być komplet:
http://pokazywarka.pl/jcu3hf/
Tak, to koniec.
mp
3×2 3×2 3×1 3xx 3xx 3xx x3x x3x 23x 23x
xxx x1x xxx x1x xxx xx1 2×1 2xx xxx xx1
x1x xxx x2x x2x x21 xx2 xxx xx1 xx1 xxx
Układów z jednym rozwiązaniem jest 10.
1×3
xxx
x2x
12x
xxx
xx3
1xx
xxx
x32
x12
xxx
3xx
1xx
xxx
x32
xxx
1xx
x32
xxx
1×2
x3x
x12
xxx
3xx
x1x
xxx
3×2
xxx
x1x
3×2
xxx
x12
3xx
Jest kilka z dwoma i trzema rozwiązaniami.
W poprzednim komentarzu dwukrotnie podałem
1xx x12
xxx xxx
x32 3xx
Powinno być
1xx
xx2
x3x
„3” na a1, „2” na c1 i c3 = 4 rozwiazania
„3” na b1, „2” na a1 i a2 = 4 rozwiazania