Moc macek

11 marca 2011
Marek Penszko

W latach 90. do najpopularniejszych rodzajów łamigłówek należała w Japonii – obok sudoku i obrazka logicznego – ściankologika (tłumacząc dosłownie japońskie określenie). W roku 1996 po raz pierwszy zmagali się z nią uczestnicy Mistrzostw Świata, po czym ochrzciłem ten typ zadania wypustkami. Na świecie zwie się różnie, ostatnio cztery wiatry lub macki. To drugie określenie widzi mi się najbardziej, więc przy nim pozostanę.

W niektórych kratkach diagramu znajdują się liczby, które mogą wysuwać macki w czterech kierunkach – w wierszach i kolumnach, czyli na boki, w dół i w górę. Wartość liczby, zwana jej mocą, oznacza, ilu pustych kratek liczba może i powinna sięgnąć mackami. Pustych pól w diagramie jest tyle, ile wynosi suma wszystkich liczb, a celem jest oznaczenie wysuniętych macek tak, aby „omacały” wszystkie puste pola. Jak z tego wynika, dwie macki nie mogą sięgnąć tego samego pola i odwrotnie.
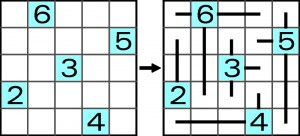
Tak to wygląda w przykładzie:

Przy odrobinie wyobraźni można dostrzec jakieś antypatyczne stwory o różnej mocy macek, przypominających „rogi” ślimaka i wysuwanych w celu opanowania terenu. Stwory nie mają się ku sobie, więc unikają… macania się. Cały taki obrazek tworzy układ jakby samorozwiązujący się w wyniku prób wysuwania macek na różne sposoby. Japończycy nazwą ściankologika sugerowali inną wizję: od pól z cyframi stawiane są murki w jednym, dwóch, trzech lub czterech kierunkach. Na polach mogłyby też stać Światowidy i sięgać wzrokiem (wzrokami 🙂 ) tak daleko, jak im liczby pozwalają. Popuściwszy wodze fantazji można by pewnie jeszcze coś wymyślić.

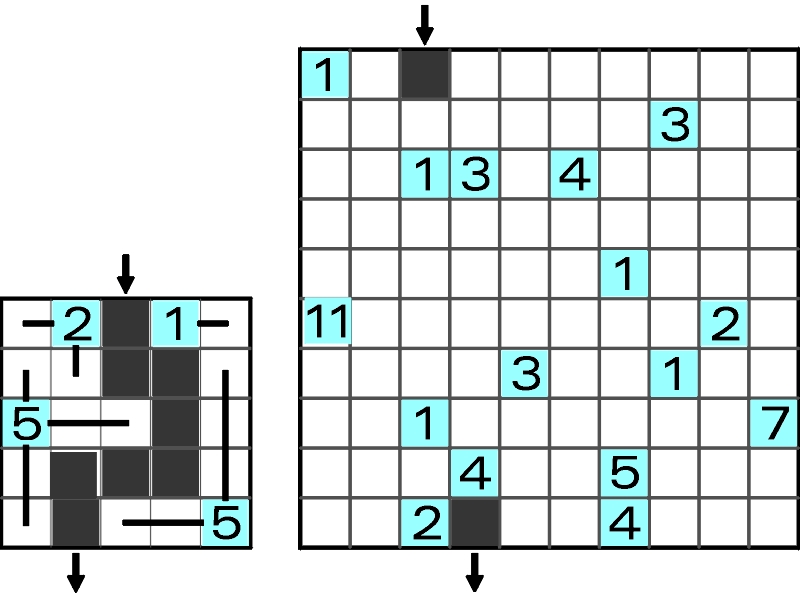
To, co popularne, zaczyna owocować wieloma odmianami. Tak też od początku było i jest nadal z mackami. Oto jedna z pierwszych odmian – z dróżką przez diagram. Sądzę, że zamiast dodatkowych wyjaśnień  wystarczy przykład:

W pierwszej chwili chciałem napisać, że jako rozwiązanie wystarczy podać długość ścieżki. Opamiętałem się jednak i proszę o podanie, ile na ścieżce jest zakrętów.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.