Para niemacana

14 marca 2011
Marek Penszko

Przesłanki są dwie:
1) każda liczba wysuwa ortogonalnie (w wierszu lub/i w kolumnie) jedną, dwie, trzy lub cztery macki, sięgające w sumie tylu pustych pól, jaka jest wartość tej liczby.
2) każdego pustego pola sięga jedna i tylko jedna macka.

Powyższe stwierdzenia to klucz do rozwiązywania macek (dokładniej o tym typie zadania – w poprzednim wpisie) i podstawa wyciągania wniosków. Ogólny, prosty wniosek jest taki, że suma liczb równa jest liczbie pustych pól.
A gdyby te sumy nie były równe, czyli gdyby na wstępie założyć, że jakiegoś pola lub pól – ale nie wiadomo których – macki nie sięgają. Pomysł takiej odmiany pojawił się dawno temu. Nie przyjął się jednak z prostego powodu: w takim układzie odpada przesłanka (2), a zadanie staje się logicznie uboższe. Nie można wówczas wnioskować np. tak: pola x musi sięgnąć macką liczba y, bo inaczej nie byłoby ono w ogóle „macane”.
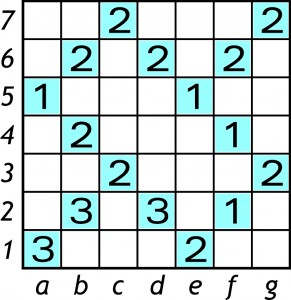
Mimo tej słabości, łamigłówki z nietkniętymi polami sporadycznie pojawiały się. Poniższa pochodzi z 10. mistrzostw Japonii (2001).

Których dwóch pól macki nie sięgają?
Proste? Trudniej i ciekawiej jest wówczas, gdy pola zostaną jakoś zdyscyplinowane, np. ulokuje się dokładnie po jednym w każdym rzędzie i kolumnie. O tym będzie jednak w majowym numerze Wiedzy i Życia, a papier, jako starszy, ma przed wirtualem pierwszeństwo.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.