Gwiazdka
Zacznę od „stłuczenia” jaj z poprzedniego wpisu.
Przetłumaczone z błędem zadanie brzmi w oryginale:
If, on average, a hen and half can lay an egg and a half in a day and a half, how many eggs at this rate would six hens lay in eight days?
Półtora dnia zostało więc w przekładzie skrócone o pół dnia. Znając tylko odpowiedź równą 32, można było oczywiście typować jeszcze dwa inne błędy – wszystkie podał zwięźle w komentarzu kroQ.
A teraz gwiazdka – trochę nietypowa, bo znacznie przedgwiazdkowa i złożona z 12 trójkątów równobocznych.
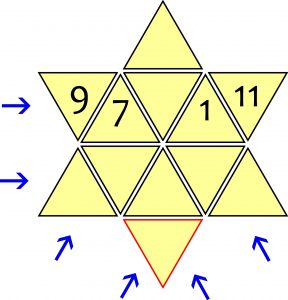
Zadanie polega na uczynieniu gwiazdki magiczną, czyli wpisaniu w trójkątne pola liczb od 1 do 12 tak, aby ich suma w każdych pięciu trójkątach tworzących rząd wskazany strzałką – była jednakowa. Łamigłówka jest mocno napoczęta – cztery liczby w jednym rzędzie są już na swoich miejscach, więc wystarczy odpowiednio ulokować osiem pozostałych. Mimo to znalezienie jedynego rozwiązania nie jest proste, zatem przyda się podpowiedź: liczby nieparzyste nigdzie więcej – poza dwiema ujawnionymi parami – nie mogą ze sobą sąsiadować, czyli znaleźć się w trójkątach sąsiadujących bokami.
W rozwiązaniu wystarczy podać liczbę, która trafi do trójkąta z czerwoną obwódką.

Komentarze
Suma 32. W czerwonym trójkącie jest 2. Od góry mamy:
12
9-7-4-1-11
3-6-8-10-5
2
2.
Niech S będzie tą jednakową sumą liczb w pięciu trójkątach ułożonych w linii. Suma wszystkich liczb w diagramie, to 12 * 13 / 2 = 78.
Niech X będzie sumą liczb z przeciwległych trójkącików (nie ważne której pary przeciwległych trójkącików – wszystkie są takie same), wtedy X + 2S = 78, czyli X = 78 – 2S, czyli X jest liczbą parzystą.
A zatem naprzeciwko liczb 9 i 11 muszą leżeć brakujące liczby nieparzyste 3 i 5. Oczywiście 5 leży naprzeciwko 9 a 3 naprzeciwko 11, bo w drugim przypadku mielibyśmy 9 + 3 = X = 11 + 5, czyli sprzeczność.
A zatem X = 14, to oznacza, że S = 32 i możemy wpisać brakującą liczbę 4 w górnym poziomym wierszu.
Do sukcesu brakuje jeszcze tylko jednego drobnego spostrzeżenia: wiersz ukośny zawierający liczby 4, 1 i 5 ma sumę S = 32. Nieznane są dwie liczby z tego wiersza, których suma wynosi 32 – 4 – 1 – 5 = 22.
Muszą to być zatem liczby 10 i 12. Dodatkowo na górze nie może być 10, bo wtedy naprzeciwko musiałaby być 4 (jako X – 10), ale 4 już jest w diagramie.
Reszta wychodzi już bez problemu.
http://pokazywarka.pl/0vtgbc/
Zadanie jest śmiesznie łatwe, a warunek o niesąsiadowaniu liczb nieparzystych niepotrzebny.
Suma liczb od 1 do 12 to 78, czyli liczba parzysta. Jest to równocześnie suma dwóch sąsiadujących ze sobą rzędów (każdy złożony z 5 liczb) i dwóch nienależących do nich wierzchołków gwiazdy. Skoro suma liczby w każdym rzędzie jest taka sama, to suma 10 liczb w dwóch rzędach musi być parzysta. A zatem również suma liczb dla każdej pary przeciwległych wierzchołków musi być parzysta i sumy te muszą być równe. W dwóch wierzchołkach mamy liczby nieparzyste (9 i 11). Na przeciwko nich muszą być 5 i 3.
Jeżeli suma liczb w przeciwległych wierzchołkach wynosi 14, to suma liczb w rzędzie musi być równa 32, bo 32+32+14=78. stąd brakującą liczbą w górnym rzędzie musi być 4. W rzędzie, wskazanym przez położoną najdalej w prawo strzałkę mamy w tym momencie liczby 1, 4 i 5 czyli w sumie 10. Żeby cały rząd miał sumę 32, suma pozostałych liczb musi być 22, czyli jest to 10 i 12. Gdyby na samej górze była liczba 10, to na dole musiałoby być 4, a 4 już została wykorzystana. Na górze musi być więc 12, a zatem rozwiązaniem zadania jest liczba 2.
Nie twierdziłem, że warunek o niesąsiadowaniu „jest potrzebny”, a tylko, że „przyda się”. Jak wynika z analizy Michała, chyba jednak przesadziłem, twierdząc, że bez tego warunku znalezienie rozwiązania nie jest proste.
mp
W dolnym trójkącie jest 2. Suma w pięciu =32
Zagadka:
Jaki tytuł nosił łamiblogowy wpis, który następował po „Między rogami”, a przed „2, 5, 9, 41, 44…” ?
Chyba powinienem wyjaśnić, że między wskazanymi wpisami były dwa wpisy, których oficjalnie już nie ma, a ściślej – z pewnych względów zmieniły się we wpisy prywatne.
mp
Najpierw oznaczenia. Kolejno rzędami brakujące liczby:
A
B
C, D, E, F, G
H
1. Parzyste muszą być na pewno B, D i F (sąsiadują z nieparzystymi). Z drugiego poziomego rzędu wynika więc, że i suma całego rzędu będzie parzysta.
2. Porównujemy dwa skośne rzędy stykające się dołami: E+F+H+12 = D+E+H+16, więc: D+4 = F.
3. Patrząc dalej na dowolny z tych dwóch rzędów (wpisane liczby dają parzystą sumę, D lub F też jest parzyste), wnioskujemy, że E i H mają taką samą parzystość, a ponieważ są sąsiadami, więc muszą być parzyste.
4. D, E, F są parzyste, więc pozostałe liczby z tego rzędu (C, G) muszą mieć taką samą parzystość. W całej gwiazdce brakuje nam dwóch nieparzystych liczb (3, 5), a nie znamy parzystości tylko C, G i F, w związku z czym C i G muszą być nieparzyste.
5. Dwa rzędy zawierające A: A+B+7+D+C=A+B+1+F+G, uwzględniając pkt. 2., dostajemy: C+2 = G, a z pkt. 4. wynika: C = 3, G = 5.
6. Znamy dwie przeciwległe liczby: 3 i 11. Pozostałe liczby tworzą dwa rozłączne rzędy. Suma wszystkich liczb w gwieździe, to 78, a bez 3 i 11: 64. Czyli suma w rzędzie wynosi 32, a B = 4.
7. Czwórka jest już zajęta, więc D+4 = F spełnią pary: (2, 6), (6, 10), (8, 12). Z niższego poziomego wiersza (pamiętając o pkt. 2.) mamy: 2*D+E=20. D nie może być dwójką, bo E będzie zbyt duże i nie może być ósemką, bo E musiałoby być czwórką. Czyli: D=6, E=8, F=10, A=12, G=2
Cała gwiazdka:
12
9,7,4,1,11
3,6,8,10,5
2
Pominięcie warunku o nieparzystych sąsiadach niczego nie zmienia, dalej jest jedno rozwiązanie.
Jedyne rozwiązanie (wierszami, bez formatowania, bo i jak ? ):
):
12
9, 7, 4, 1, 11
3, 6, 8, 10, 5
2
Dzielimy gwiazdę na 2 zbiory, 6 pól wewnętrznych i 6 zębów zewnętrznych.
Generujemy wszystkie podziały spełniające warunki logiczne.
Okazuje się, że jest ich 2.
Te kilka możliwości ulokowania podzbiorów sprawdzamy ręcznie.
Czasami czytałem Łamiblog, ale jakoś nigdy nie zabierałem się za rozwiązywanie zadań. No cóż kiedyś musi być pierwszy raz
Poszło niespodziewanie łatwo:
12
9 7 4 1 11
3 6 8 10 5
2
Trójkąt w ramce 2.
Pozostałe od góry;
12,
9,4,1,11,
3,6,8,10,5,
2.
Pozdrawiam.
Muszę nanieść poprawkę.
Trójkąt w ramce 2.
Pozostałe od góry;
12,
9,7,4,1,11,
3,6,8,10,5,
2.
Pozdrawiam.
12
9 7 4 1 11
3 6 8 10 5
2
Jest tylko 6 podstawowych różnych rozwiązań (bez symetrii i obrotów – rozwiązanie zadania to c. ).
a)
1
2 12 9 6 4
8 3 5 7 10
11
b)
2
1 9 12 3 8
4 6 7 5 11
10
c)
2
3 6 8 10 5
9 7 4 1 11
12
d)
3
2 8 6 7 9
5 10 1 4 12
11
e)
4
1 9 6 7 10
2 12 3 5 11
8
f)
5
2 8 10 1 11
3 6 7 4 12
9
Ale miło mi się zrobiło, gdy zobaczyłem swój pogrubiony nick
Odpowiedź do tej zagadki: 2
Należy spostrzec, że pod 7 i 1 będą odpowiednio X i X+4. Wypisać wszystkie możliwe pary a następnie zorientować się, że 3 i 5 mogą być tylko w rogach płd.-wsch. i płd.-zach. ze względu na parzystą magiczną sumę. Dalej idzie się jak po sznurku.
2
W trójkącie z czerwoną obwódką jest: 2. A suma w zaznaczonych rzędach jest 32. I nie korzystałam z dodatkowej informacji o liczbach nieparzystych. Wystarczyło zauważyć, że w prawoskośnym rzędzie od górnego trójkąta idąc, suma trzech liczb (poza środkową – dowolną zresztą – w pierwszym poziomym rzędzie) zawsze jest 27 i musi się składać z 12, 10 i 5. Reszta już poszła gładko