Sud/oku
Sudoku od dawna nie jest z mojej bajki z prostego powodu – przejadło mi się. Czasem jednak trafiam na jakiś wariant, który ma w sobie coś, więc z czystej ciekawości zabieram się za konsumpcję. Ostatnio Michał S. podesłał mi sudoku ułamkowe swojego pomysłu, które jest na tyle osobliwe i ciekawe, że zasługuje na ekspozycję w Łamiblogu. Zanim jednak to nastąpi, chciałbym przedstawić „klasyczną” odmianę sudoku ułamkowego – nienową, ale bardzo rzadko goszczącą w przestrzeni wirtualnej i papierowej.
Instrukcja obsługi wydaje się zbędna, bo podstawowe zasady sudoku są ogólnie znane, a dotyczących rzeczonej odmiany łatwo domyślić się z przykładu 6×6:
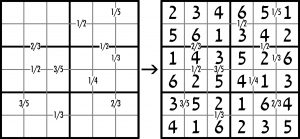
W zadaniu zakres mianowników i liczników jest oczywiście większy:

W rozwiązaniu wystarczy podać sumę cyfr na „spłonionej” przekątnej.
Uwaga: zadanie (diagram) poprawione 16.11; 21.55 – dodany jeden ułamek, aby było jedno rozwiązanie (mam nadzieję, że jest).
![]()

Komentarze
A mnie się sudoku nie przejadło. Przy czym nigdy nie sięgam po to zwykłe. Lubię wyłącznie killer sudoku oraz greater than killer sudoku. Korzystam z tej strony:
http://www.dailykillersudoku.com/main/past_puzzles/
Ta łamigłówka jest też niezła w odmianie irregular, czyli z polami w nieregularnych kształtach. Nie mam ulubieńszej od 10 lat już chyba. Ciekawe, czy natrafię kiedyś na coś, co ją zdetronizuje 🙂
Wychodzi kilka rozwiązań:
http://pokazywarka.pl/onckui/
Zadanie wydaje się niejednoznaczne bo jest parę par miejsc przemiennych, ja widzę 4 rozwiązania:
3 7* 4 8 5 1* 1 5 2
3 2* 4 8 5 1* 1 5 2
3 7* 4 8 5 2* 1 5 2
3 1* 4 8 5 2* 1 5 2
W pierwotnej wersji zadanie ma 5 rozwiązań
591348762
682917354
437526189
168432597
743659821
925871436
814293675
276185943
359764218
591348762
682917354
437526189
168432597
743659821
925871436
874293615
216785943
359164278
591348762
682917354
437526189
268431597
743659821
915872436
824193675
176285943
359764218
591348762
682917354
437526189
268431597
743659821
915872436
824793615
176285943
359164278
591348762
682917354
437526189
268431597
743659821
915872436
874293615
126785943
359164278
W poprawionej 2
591348762
682917354
437526189
268431597
743659821
915872436
824793615
176285943
359164278
591348762
682917354
437526189
268431597
743659821
915872436
824193675
176285943
359764218
Aby miało 1 rozwiązanie należy przykładowo wstawić ułamek 1/7 albo 2/7 w drugiej kolumnie pomiędzy 6 i 7 wierszem
Chciałem uniknąć takiego „jednoznacznego” ułamka, ale chyba jednak się nie da.
mp
Rozwiązanie jest jedno: suma pól na przekątnej jest 36. Ale samo sudoku ma dwa rozwiązania.
W IV i VIII kolumnie , a I i III wierszu jest 1 lub 7 zamiennie.
Przekątna zawiera liczby : 3,7,4,8,5,1,1,5,2
Podaję cały układ rozwiązania, bo mam wątpliwości:
591348762
682917354
437526189
268431597
743659821
915872436
824x936x5
176285943
359x642x8
W dolnej części diagramu widać cztery znaki x, które zastępują 1 i 7 – są dwie możliwości ich wstawienia.
Wiem o dodatkowym ułamku, ale on tu nic nie zmienia.
Mój błąd, czy zadanie wciąż wymaga zmiany?
Rozwiązania są dwa, czyli w rozwiązaniu błędu nie ma.
mp
@OlaGM
Skoro już pojawiają się linki do rozważenia, to na chwilę chyba można wpaść tu:
http://gameaboutsquares.com/
@Apartado
To jest super! Muszę też moim dzieciom pokazać.
Odmiana Sokobana 🙂 Wciągające.
mp
Suma na przekątnej 36.
Ale całe sudoku ma dwa rozwiązania – cyfry 1 i 7 można zamienić w 7 i 9 wierszu oraz 4 i 8 kolumnie.
Są dwa rozwiązania.
Jest albo (A,B)=(1,2) albo (A,B)=(2,1)
5,9,1,3,4,8,7,6,2
6,8,2,9,1,7,3,5,4
4,3,7,5,2,6,1,8,9
A,6,8,4,3,B,5,9,7
7,4,3,6,5,9,8,2,1
9,B,5,8,7,A,4,3,6
8,A,4,B,9,3,6,7,5
B,7,6,A,8,5,9,4,3
3,5,9,7,6,4,2,1,8
Da się zrobić ręcznie, bez rozwidleń 🙂
Rozwiązania istotnie są dwa, ale nie takie (uwzględniając poprawkę, czyli dodany ułamek 1/4).
mp
Nie zauważyłem poprawki 🙂
Jedyne rozwiązanie to:
5,9,1,3,4,8,7,6,2
6,8,2,9,1,7,3,5,4
4,3,7,5,2,6,1,8,9
2,6,8,4,3,1,5,9,7
7,4,3,6,5,9,8,2,1
9,1,5,8,7,2,4,3,6
8,2,4,1,9,3,6,7,5
1,7,6,2,8,5,9,4,3
3,5,9,7,6,4,2,1,8
Rozwiązania są jednak dwa: cyfry 1 i 7 można zamienić miejscami w 7 i 9 wierszu oraz 4 i 8 kolumnie.
mp