Sudoku Fareya
Zapowiedziane przed tygodniem sudoku ułamkowe Michała S. jest dość „awangardowe”, bowiem – jak napisał autor – niemal każdą liczbę wpisuje się w nim do diagramu „po kawałku”. Ułamki, które w wersji sprzed tygodnia stanowiły podpowiedzi umieszczane na granicach pól, tym razem pojawiają się polach zamiast typowych dla sudoku cyfr od 1 do 9. Inaczej mówiąc, do pól wpisuje się dziewięć początkowych wyrazów ciągu ułamków właściwych dodatnich, który powstaje w następujący algorytmiczny sposób:
(1) piszemy dwa początkowe ułamki – 1/2 i 1/3
(2) licznik każdego kolejnego ułamka wzrasta o 1 dotąd, aż będzie o 1 mniejszy od mianownika
(3) mianownik następnego ułamka wzrasta o 1, a licznik zmienia się w 1
(4) powrót do (2)
Ułamki skracalne pomijamy, więc ostatecznie ciąg przybierze postać:
1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 5/6, 1/7, 2/7, 3/7, 4/5,… Wytłuszczone wyrazy „uczestniczą” w sudoku. Można je określić jako wszystkie nieskracalne ułamki właściwe o mianowniku nie większym niż 5. Albo ściślej matematycznie: są to wyrazy ciągu Fareya rzędu 5 – wszystkie oprócz skrajnych. Warto też zauważyć, że liczniki i mianowniki tych ułamków tworzą dwa odrębne ciągi liczb naturalnych uwzględnione w OEIS jako A020652 i A038567.
Wracając do sudoku, podpowiedziami są w nim litery umieszczone na granicach pól. Oznaczają one, że ułamki w sąsiednich polach mają jednakowe liczniki (litera L) lub mianowniki (M). Uwzględnione są wszystkie takie sąsiedztwa, a więc jeśli między polami nie ma litery, to liczniki ułamków w tych polach są różne i mianowniki także.
W poniższej łamigłówce na dobry początek ujawniony jest tylko jeden ułamek – w lewym górnym rogu.
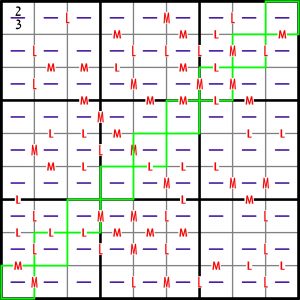
Autor zadania ufundował nagrodę, grę „Rachmistrz„, do rozlosowana wśród osób, które nadeślą poprawne rozwiązanie – wystarczy podać sumę ułamków na „pozieleniałej” przekątnej.
Uwaga: o 10.35 (23.11) naniesiona poprawka (usunięte L z 4. rzędu między polami 8 a 9).

Komentarze
„Uwzględnione są wszystkie takie sąsiedztwa” – czy na diagramie nie ma zatem błędu? W 5. rzędzie między polami 8. a 9. także spodziewałabym się L.
Albo czegoś nie rozumiem, albo coś jest nie tak z L-kami w rzędach 7., 8. i 9. od góry. Cztery L wskazują na licznik 1, który przechodzi także do rzędu 4. A tam skupisko L również wskazuje na licznik 1, ale sąsiedztwo nie jest zaznaczone.
Pani Olu, naniosłem poprawkę, która miała związek z Pani poprzednią uwagą (dziękuję), ale w przypadku powyższej uwagi nie mam co poprawiać, czyli wszystko jest OK.
mp
Ale zakręcone zadanie 🙂 Wynik: 73/15
http://pokazywarka.pl/evm6oe/
Uwaga nr 2 też była do starej wersji diagramu.
2/5+1/3+3/5+2/3+3/5+4/5+1/5+2/3+3/5=73/15
KODujemy 😉 dla większej przejrzystości obrazka:
1=1/2
2=1/3
3=2/3
4=1/4
5=3/4
6=1/5
7=2/5
8=3/5
9=4/5
Są dwa rozwiązania:
(A,B)=(1,4) albo (A,B)=(4,1)
3,6,2,5,9,7,A,B,8
8,5,9,4,1,6,2,3,7
1,4,7,2,3,8,6,9,5
5,3,6,7,2,9,B,8,A
9,7,4,6,8,1,3,5,2
2,8,1,3,5,4,7,6,9
4,1,8,9,6,2,5,7,3
6,2,5,8,7,3,9,A,B
7,9,3,1,4,5,8,2,6
Rozwiązanie jest jedno. Proszę uważnie przyjrzeć się ewentualnej zamianie miejscami A i B w czwartym wierszu.
mp
Niech mnie gęś……ale nie widzę o co chodzi 🙁 Dla mnie są dwa rozwiązania jak byk i dalej ściana, gdyż sugerowana zamiana w 4 wierszu pociąga za sobą zamiany w wierszach 1 i 8 a parę (A,B) możemy skonstruować na 2 sposoby. Ale w środę wszystko się wyjaśni 🙂
Gdyby w 9. polu 4 wiersza było 1/4 to wtedy między tym polem a polem nad nim powinno być M.
mp
Suma ułamków na przekątnej… 73/15, czyli 4 i 13/15
Nie taki diabeł straszny. Aczkolwiek nie obyło się bez kreśleń i poprawek. Suma zielonej przekątnej to 4.87
Rozwiązanie: http://bankfotek.pl/view/2103630
Czasami warto przeczytać instrukcję obsługi młynka do kawy nawet jeśli umiemy mielić kawę 😉 A więc: (A,B)=(1,4).
Jeśli chodzi o grę Rachmistrz to wydaje się być ona niezwykle elitarna gdyż, przy obecnych standardach, obciążenie umysłu już tylko 4 działaniami na 2 liczbach, wykonywanymi na czas, wydaje się być skierowane do osób z obszaru powyżej 3 sigma, szczególnie w wersji ułamkowej. Przy przejściu z 2 kostek na 3 mamy lawinowy wzrost ilości możliwych działań. Tytuł gry trafiony idealnie 😉
Suma to w ułamku niewłaściwym 73/15. Samo sudoku ma 2 rozwiązania.
Wracam honor, rozwiązanie sudoku jest dokładnie jedno.
Odpowiedź: 4 i 13/15
Fajne zadanie, szybko się rozwiązuje, ale oczy puchną od patrzenia na gryzmoły 🙂
Wiadomo, że grupy L (więcej, niż dwie w rzędzie) mogą utworzyć tylko cyfry 1, a M tylko cyfry 5, więc szybko w całym diagramie można wypełnić wszystkie ich wystąpienia. Wtedy w każdym kwadracie 3×3 pozostają tylko dwa zupełnie puste pola, w których będą 2/3 i 3/4. Dalej już prosto. Tylko te oczy 😉
Suma ułamków na przekątnej to 4 całe i 13/15
Pełne rozwiązanie:
2/3 1/5 1/3 3/4 4/5 2/5 1/2 1/4 3/5
3/5 3/4 4/5 1/4 1/2 1/5 1/3 2/3 2/5
1/2 1/4 2/5 1/3 2/3 3/5 1/5 4/5 3/4
3/4 2/3 1/5 2/5 1/3 4/5 1/4 3/5 1/2
4/5 2/5 1/4 1/5 3/5 1/2 2/3 3/4 1/3
1/3 3/5 1/2 2/3 3/4 1/4 2/5 1/5 4/5
1/4 1/2 3/5 4/5 1/5 1/3 3/4 2/5 2/3
1/5 1/3 3/4 3/5 2/5 2/3 4/5 1/2 1/4
2/5 4/5 2/3 1/2 1/4 3/4 3/5 1/3 1/5