Resztoku
Do trzech razy sztuka, czyli zdecydowałem się przedstawić trzecie z serii odmian sudoku podobnego rodzaju. Podobieństwo polega na umieszczaniu podpowiedzi na granicach między polami. Poprzednio w tych miejscach pojawiały się ułamki lub informacje dotyczące ułamków, które były wpisywane w pola. Tym razem podpowiedzi wiążą się z dzieleniem: liczba na granicy dwóch pól jest resztą z dzielenia większej z pary liczb, które powinny trafić do tych pól, przez mniejszą. Zero oznacza oczywiście, że mniejsza liczba jest dzielnikiem większej.
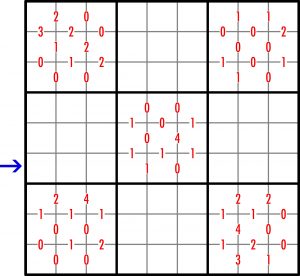
Zadanie wydaje się dość trudne. Jednoznaczne są tylko jedynki, dalej zaczynają się schody. Ciekawe, czy możliwe jest usunięcie jakiejś podpowiedzi bez utraty jednoznaczności rozwiązania.
Jako rozwiązanie końcowe wystarczy podać kolejne liczby w wierszu wskazanym strzałką.

Komentarze
312 784 965
Pełne rozwiązanie wraz ze ściągawką jest tu:
http://pokazywarka.pl/6ce4wb/
312 784 965
Kolejne cyfry ze wskazanego rzędu od lewej do prawej to: 3 1 2 7 8 4 9 6 5
Gdybym nie rozpisał sobie wszystkich możliwych ułamków dla każdej z reszt, stwierdziłbym, że zadanie jest bardzo trudne. Ale rozpisałem sobie i zajęło ok. godziny (w tym cofałem ze dwa razy z powodu błędów).
Odpowiedź: 312784965
Najlepiej rozpocząć od dwóch kwadratów 3×3 zawierających czwórki (tam może być wyłącznie para 5-9). Po kolei da się wypełnić jednoznacznie wszystkie narożne kwadraty. Później środkowy (częściowo) i zostaje zabawa z pustymi. Ale do samego końca da się rozwiązać bez zgadywania.
Czy możliwe jest usunięcie jakiejś podpowiedzi bez utraty jednoznaczności rozwiązania?
Tak, można usunąć niektóre cyfry. Na przykład w prawym górnym kwadracie 3×3 w jego środku można wstawić jedynkę bez względu na to, czy cztery zera otaczające środkowe pole tam będą, czy ich tam nie będzie.
Przypuszczam, że w podobny sposób można usunąć wiele cyfr podpowiedzi z innych miejsc resztoku.
Ciekawym wydaje mi się inny, bardziej ogólny, problem.
Wiemy (albo przypuszczamy), że w zwykłym klasycznym sudoku musi być co najmniej 17 cyfr, aby rozwiązanie było jedno.
A jak powyższy problem wygląda w resztoku?
Jaka jest minimalna ilość cyfr podpowiedzi, aby uzyskać jednoznaczność rozwiązania?
Natknąłem się na dzieldoku w innej formie:
http://digitaleditions.walsworthprintgroup.com/publication/?i=443582#{%22issue_id%22:443582,%22page%22:24}
Jakoś nie znalazłem czasu/ochoty/inne*, żeby się nad tym pochylić, ale może kogoś zainteresuje/zainspiruje/inne*.
*niepotrzebne skreślić 🙂
Jest tylko jedno rozwiązanie:
9,7,1,4,3,8,2,5,6
6,5,3,9,2,7,8,1,4
2,4,8,5,6,1,7,3,9
5,8,9,2,1,6,3,4,7
4,6,7,3,9,5,1,2,8
3,1,2,7,8,4,9,6,5
7,9,5,1,4,2,6,8,3
8,2,4,6,7,3,5,9,1
1,3,6,8,5,9,4,7,2