Królewska królówka
Zadania takie, jak poniższe zwane są czasem królówkami.
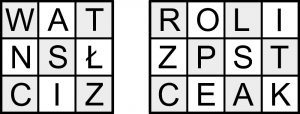
Z danego diagramu należy odczytać jakieś słowo lub krótki tekst, wędrując po polach ruchem króla szachowego, czyli przechodząc z pola na sąsiednie pole – w wierszu, w kolumnie lub na ukos. Kolejno „zaliczane” litery powinny być kolejnymi literami tekstu. W diagramie 3×3 ukrywa się imię i nazwisko STANISŁAW STASZIC, w diagramie 3×4 – nazwa RZECZPOSPOLITA POLSKA.
Ułożenie ambitnej królówki to częściowo kwestia przypadku. „Ambitnej” oznacza, że różnych liter jest tyle, co pól prostokątnego diagramu, a ich układ w odczytywanym tekście jest taki, że tekst da się wcisnąć w graf królewski.
Ostatnio ślęczałem nad naszym ostatnim królem. STANISŁAW AUGUST PONIATOWSKI ma tuzin różnych liter, więc kusi, aby spróbować upchnąć go w diagramie 3×4. Niestety, łatwo sprawdzić, że to niemożliwe. Proponuję więc pogimnastykować umysł nad królówką poniekąd mniej ambitną, polegającą na ulokowaniu ostatniego króla w kwadracie 4×4. Niektóre litery mogą się w diagramie powtórzyć, ale powtórzeń powinno być jak najmniej, czyli niektóre z 16 pól pozostaną puste. Czy komuś uda się nie umieścić liter w więcej niż jednym polu?

Komentarze
Oczywiście litera X oznacza pole puste. 3 puste pola:
XXSK
XWIŁ
ONAG
PTSU
STPO
OUAN
GWŁI
__SK
„Wspomogłem” się tutaj programem. Diagramu bez trzech liter nie znalazłem.
Diagram bez 3 liter istnieje.
mp
KSŁ_
INWA
APOU
_TSG
Mi wyszło że 13 to minimalna liczba pól na której uda się upchnąć ostatniego król.
Poniżej przykładowy diagram:
G S T P
U A N O
Ł I W
S K
Nie wiedzieć czemu zjadło mi spację w ostatnim rzędzie. Może tak będzie lepiej.
G S T P
U A N O
Ł I W _
_ S K _
Jest 25 rozwiązań z trzema pustymi polami (oznaczonymi X).
21 z nich ma początkowe S w pozycji (2,2) a 4 w pozycji (1,2).
Te z S w pozycji (2,2) mają warianty symetryczne, więc wyrzuciłem je, co widać po lukach w numeracji.
Liczby w prawym dolnym rogu pokazują położenie ostatniej litery I w zlinearyzowanej wierszami tablicy.
Ciekawe jakby to poszło ruchem skoczka 🙂
1
„L”,”W”,”T”,”P”
„A”,”S”,”O”,”A”
„U”,”K”,”I”,”N”
„G”,”X”,”X”,”X”,11
„—————-”
2
„L”,”W”,”T”,”P”
„A”,”S”,”O”,”A”
„U”,”K”,”I”,”N”
„X”,”G”,”X”,”X”,11
„—————-”
3
„L”,”K”,”I”,”A”
„A”,”S”,”T”,”N”
„U”,”W”,”O”,”P”
„G”,”X”,”X”,”X”,3
„—————-”
4
„L”,”K”,”I”,”A”
„A”,”S”,”T”,”N”
„U”,”W”,”O”,”P”
„X”,”G”,”X”,”X”,3
„—————-”
5
„L”,”W”,”O”,”P”
„A”,”S”,”T”,”N”
„U”,”K”,”I”,”A”
„G”,”X”,”X”,”X”,11
„—————-”
6
„L”,”W”,”O”,”P”
„A”,”S”,”T”,”N”
„U”,”K”,”I”,”A”
„X”,”G”,”X”,”X”,11
„—————-”
13
„L”,”K”,”I”,”N”
„A”,”S”,”O”,”A”
„U”,”W”,”T”,”P”
„G”,”X”,”X”,”X”,3
„—————-”
14
„L”,”K”,”I”,”N”
„A”,”S”,”O”,”A”
„U”,”W”,”T”,”P”
„X”,”G”,”X”,”X”,3
„—————-”
15
„L”,”K”,”X”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„G”,”P”,”O”,”X”,7
„—————-”
16
„L”,”X”,”K”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„G”,”P”,”O”,”X”,7
„—————-”
17
„L”,”K”,”X”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„G”,”X”,”O”,”P”,7
„—————-”
18
„L”,”X”,”K”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„G”,”X”,”O”,”P”,7
„—————-”
19
„L”,”K”,”X”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„X”,”G”,”O”,”P”,7
„—————-”
20
„L”,”X”,”K”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„X”,”G”,”O”,”P”,7
„—————-”
21
„X”,”L”,”K”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„G”,”P”,”O”,”X”,7
„—————-”
22
„X”,”L”,”K”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„G”,”X”,”O”,”P”,7
„—————-”
23
„X”,”L”,”K”,”X”
„A”,”S”,”I”,”A”
„U”,”W”,”T”,”N”
„X”,”G”,”O”,”P”,7
„—————-”
24
„U”,”G”,”K”,”X”
„A”,”S”,”I”,”A”
„L”,”W”,”T”,”N”
„X”,”P”,”O”,”X”,7
„—————-”
25
„U”,”G”,”K”,”X”
„A”,”S”,”I”,”A”
„L”,”W”,”T”,”N”
„X”,”X”,”O”,”P”,7
„—————-”
26
„G”,”U”,”K”,”X”
„A”,”S”,”I”,”A”
„L”,”W”,”T”,”N”
„X”,”P”,”O”,”X”,7
„—————-”
27
„G”,”U”,”K”,”X”
„A”,”S”,”I”,”A”
„L”,”W”,”T”,”N”
„X”,”X”,”O”,”P”,7
„—————-”
43
„U”,”S”,”T”,”P”
„G”,”A”,”N”,”O”
„L”,”I”,”W”,”X”
„K”,”S”,”X”,”X”,10
„—————-”
44
„U”,”S”,”T”,”P”
„G”,”A”,”N”,”O”
„L”,”I”,”W”,”X”
„X”,”S”,”K”,”X”,10
„—————-”
45
„G”,”S”,”T”,”P”
„U”,”A”,”N”,”O”
„L”,”I”,”W”,”X”
„K”,”S”,”X”,”X”,10
„—————-”
46
„G”,”S”,”T”,”P”
„U”,”A”,”N”,”O”
„L”,”I”,”W”,”X”
„X”,”S”,”K”,”X”,10
„—————-„
SŁUG
IASK
NTWI
PO
Powtarzają się litery „I” oraz „S”.
Z szesnastu pól dwa pozostają niewykorzystane.
Osiem pierwszych słów inwokacji do „Pana Tadeusza”.
Z powtórzeniami liter „J” oraz „E”.
Litera „Ś” zastąpiona przez „S” – (bez kreski).
JEKCD
SAJZR
ETYON
LIWM_
Sprawdziłem dla konika szachowego i niestety nie da się wpisać „całego” króla.
Wszystkie podejścia kończą się na 17 literach: STANISLAWAUGUSTPO
To mi przypomina słynną anegdotę z czasów milicji obywatelskiej. Na murze w pewnym miejscu widniał przez jakiś czas napis: Katyń po
Potwierdzał on (urwany napis) powszechną opinię o zdolności MO do błyskawicznego reagowania, wyrażoną w dowcipie: Jedzie dwóch milicjantów i wpadają na drzewo. Jeden mówi do drugiego: Popatrz, jeszcze nigdy nie byliśmy tak szybko na miejscu wypadku ! 😉
Przyjemna łamigłówka, za pierwszym razem, gdy udało mi się zmieścić króla w diagram 4×4, dostałem dwa wolne kwadraty.
ŁIK_
SANS
UTWO
GOP_
Podobnie jak RZECZPOSPOLITA POLSKA, ciąg: STANY ZJEDNOCZONE USA też daje się upchnąć do diagramu 3×4.
Elegancko – bez powtórzeń i pustych pól – czyli „ambitnie”.
Ja zaproponuje coś ambitnego:
Czy istnieje diagram skończonych rozmiarów, w którym da się odnaleźć dowolne słowo (słowo, tj. dowolny ciąg liter z ustalonego alfabetu).
Proponuję zacząć poszukiwania od alfabetow z mniejszą liczbą liter, już dla 5-literowych robi się ciekawie.
Warto rozważyć dwie wersje zadania, w których w w ciagach moga/nie mogą występować koło siebie dwie jednakowe litery.
Dla 5-literowego alfabetu, bez jednakowych sąsiednich liter (X to puste miejsce):
XCDEX
EABCA
BDEDB
ACBAE
XEDCX
Dla 4-literowego alfabetu, z jednakowymi sąsiednimi literami:
XDDX
ABCA
ACBA
XDDX
Dla 5-literowego alfabetu, bez jednakowych, sąsiednich liter, wynik można poprawić, wyrzucając to E ze środka. Mamy więc pierścień:
_CDE_
EABCA
BD_DB
ACBAE
_EDC_
@Spytko
Ja ograniczylem się do próby znalezienia ogólnego schematu, który byłby dobry dla dowolnie dużego alfabetu. Niestety niczego nie udało mi się osiągnąć…
Zastanawiam się, czy to w ogóle możliwe. Intuicja podpowiada mi że tak (dla dowolnie dużego alfabeu) ale nie mam pojęcia jak tego dowieść;)
@miodziu
Niech:
ilość liter w alfabecie=k
długość słowa=n
ilość wszystkich słów długości n=k^n
Wygląda na to, że do pewnej wartości k istnieje diagram skończonych rozmiarów dla każdego słowa dowolnej długości.
Po przekroczeniu tej granicy (k), wraz ze wzrostem długości słowa (n), diagram musi się rozrastać.
Ze wzrostem n do nieskończoności diagram też musi stać się nieskończony.
Powstaje jednak pytanie czy w nieskończoności (n=nieskończoność=N=moc zbioru liczb naturalnych), może on być jeszcze diagramem, czyli przeliczaną tablicą (przeliczalny tzn. równoliczny ze zbiorem liczb naturalnych).
Okazuje się, że nie może. Z tw. Cantora wynika, że zbiór mocy 2^N ma moc ostro większą niż N.
Nasz zbiór ma K^N elementów, czyli na pewno nie mniej niż 2^N.
Oznacza to, że elementów tych zbiorów nie da się ustawić w pary biorąc po jednym z każdego z nich.
Nasz zbiór słów ma ciekawą własność. Dla skończonego n ma skończoną moc. Dla n=N ma moc ostro większą od N i nie da się go ustawić w nieskończoną listę.
Przypadkiem się złożyło, że łamigłówka o kanibalach i niekanibalach (którą podrzuciłem w Łamiblogu z 21 marca – Polidoku), dotyczy właśnie tego triku wykorzystanego do dowodu tw. Cantora 😉
@Spytko
Twój wpis mnie olśnił…
Niech alfabet będzie co najmniej 9 literowy (k >= 9). Rozważmy dowolny diagram zawierający C pól.
Rozważamy n literowe słowa rozpoczynające się ustaloną literą, które da się odnaleźć w diagramie. Pierwsze pole możemy wybrać spośród co najwyżej C liter, w każdym kolejnym kroku przechodzimy do jednego z 8 sąsiadów. Zatem liczba tych słów nie przekracza C * 8^(n-1).
Z drugiej strony, liczba wszystkich słów n literowych z ustaloną pierwszą literką to k^(n-1), co dla dostatecznie dużego n jest większe od powyższej wartości.
To pokazuje, że już dla 9-literowego alfabetu taki diagram nie istnieje. Podejrzewam również, że dla k=8 również dałoby się udowodnić nieistnienie takiego diagramu.
A co dla k=7. Intuicja podpowiada mi, że się da, choć zapewne diagram ten byłby sporych rozmiarów…
Ja rozumowałem tak: k=10 nie może być bo jeśli startujemy z jakiejś litery (przyjmijmy, że A) WEWNĄTRZ diagramu , to w otoczeniu tego A możemy mieć w najlepszym razie 8 innych liter (załóżmy, że są to: B,C,D,E,F,G,H,I i mamy jeszcze J).
Wśród wszystkich słów zaczynających się na A mamy nieskończenie wiele słów, których druga litera to właśnie J którego nie ma w otoczeniu tego startowego A.
Druga możliwość to Start z A znajdującego się NA BRZEGU obszaru. Wśród naszych słów zawsze znajdziemy takie, że kolejna litera nie występuje w otoczeniu tego A. I tak dalej tzn. zawsze mamy w kapeluszu słowo z kolejną
literą taką, której nie ma w otoczeniu tej ostatniej i musimy rozszerzać nasz obszar o jedną literę.
Proces ten nigdy się nie skończy, więc obszar nie może być ograniczony.
Dobrze, że tego nie napisałem bo wymyśliłeś inne (kombinatoryczne, ilościowe) uzasadnienie, nie odwołujące się do faktu, że słowa są nieskończone tylko dowolnie długie ale skończone 🙂
Pozostaje jednak k=6, 7, 8. Ja czarno widzę sprawę już dla k=6 🙁