Zworka
Na studiach miałem kolegę, którego ulubione powiedzonko utkwiło mi w pamięci: „myślenie to najgorsza choroba, bo nieuleczalna”. Ta sentencja przypomina mi się zwykle przy okazji tematu: dlaczego ludzie lubią rozwiązywać zagadki. Wyszła spod pióra Remarque’a – znajduje się w powieści Trzej towarzysze i pada w kontekście głębszych rozważań o sprawach ostatecznych, więc kojarzenie jej z rozrywkowym główkowaniem wydaje się trochę niestosowne. A jednak wygląda na to, że rozwiązywanie zagadek, łamigłówek, zadań, problemów – nawet tych bardzo trudnych, ale jednak rozpatrywanych bezinteresownie – jest swego rodzaju lekiem objawowym na wspomnianą chorobę. A nawet czymś więcej, bo wówczas myślenie przestaje „doskwierać”, a zaczyna sprawiać przyjemność. Zdarza się również, że popularne rozrywki umysłowe, np. krzyżówki lub sudoku, są nie tylko formą relaksu, ale przede wszystkim antidotum, przynoszącym ulgę w trudnych sytuacjach, ułatwiającym oderwanie się od kłopotów lub zmartwień – skutecznym jakby anestetykiem lub „narkotykiem”. Kto wie, czy często nie jest to ich ważniejsza funkcja, niż z reguły stawiana na pierwszym planie gimnastyka szarych komórek.
Z drugiej strony bywa, że lekarstwo staje się gorsze od choroby – gdy hobby zmienia się w obsesję. To wprawdzie rzadki przypadek, ale wśród osób, które zajmują się łamigłówkami lub grami umysłowymi profesjonalnie lub raczej półprofesjonalnie – jednak dość częsty. Niekiedy od myślenia nad czymś trudno się uwolnić i wtedy sięga się po tradycyjne lekarstwa, np. na bezsenność.
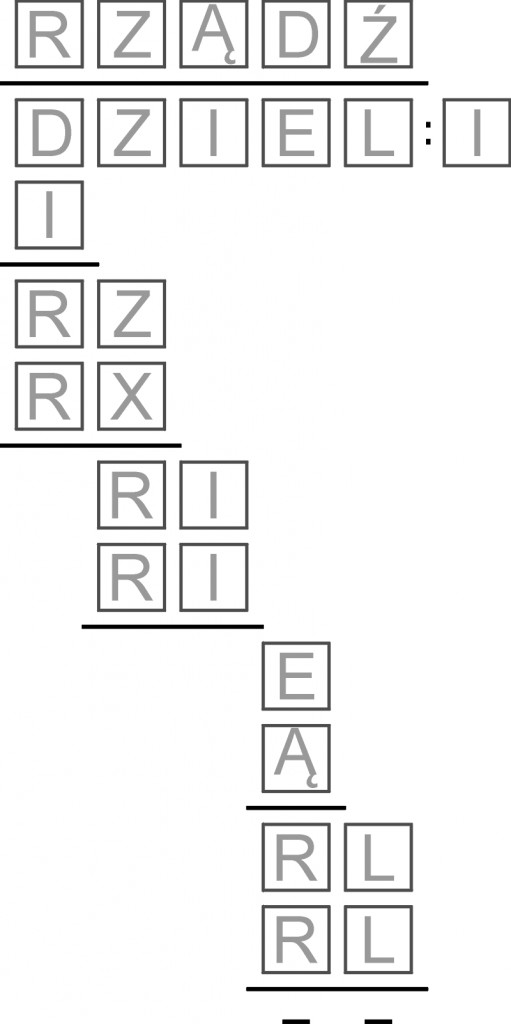
Zajmuję się m. in. układaniem krzyżówek i w związku z tym miewam do czynienia z przysłowiami, porzekadłami lub aforyzmami, które bywają ich dodatkowym rozwiązaniem. Przejawem wspomnianej obsesji, ale w łagodnej postaci, jest to, że widząc takie krótkie zdania (chyba można je zaliczyć do frazeologizmów), niemal odruchowo sprawdzam, czy któreś z nich nie nadałoby się na kryptarytm. Ta obsesyjka została mi z zamierzchłych czasów, gdy kryptarytmy były popularne, a programy do ich rozwiązywania i komputery osobiste – jeszcze nie. Pamiętam jedną perełkę sprzed lat:
DZIEL : I = RZĄDŹ
Przypomnę, że chodzi o zastąpienie liter cyframi tak, aby powstałe liczby tworzyły poprawną równość; takim samym literom powinny odpowiadać jednakowe cyfry, a różnym – różne.
Zadanie jest perełką, bo ma jedno rozwiązanie, ale równocześnie nią nie jest, bo rozwiązywanie przypomina szukanie igły w stogu siana. Dopiero w pełnym zapisie, w postaci słupka z iloczynami cząstkowymi, dzielenie staje się łamigłówką logiczną – i to dość prostą:
Ostatnio wpadłem na inny kryptarytm-porzekadło – WYSZŁO SZYDŁO Z WORKA – ale zapisany trochę dziwnie:
Piszemy o tym, co ważne i ciekawe
Psychobiznes
Od dziesięcioleci trwają znojne prace nad ustawą dotyczącą usług psychoterapeutycznych w Polsce. Dlaczego się nie udaje? Bo chodzi o pieniądze.
Jeśli przymknąć oko na „zworkę” czyli małą zworę, to perełka jest cenniejsza niż „dziel i rządź”, bo nie dość, że rozwiązanie jest jedno, to różnych liter, a więc także cyfr, mamy dziesięć. Czy jednak do jedynego rozwiązania można dojść logicznie „na piechotę” bez samoudręki lub zgrzytania zębami? Oto jest pytanie.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.


Komentarze
172469 +
247069 =
419538
Tak migiem na piechotę? A jeśli tak, to z grubsza jak?
mp
39270 : 2 = 19635
drugie trudniejsze
Rozwiązanie dziel i rządź to:
39270/2=19635
1) 39270:2=19635
2) 063459+346259=409718 (na piechotę, ale najpierw analizowanie przypadków sum: w+s=z albo w+s+1=z oraz y+z=w albo y+z+1=w albo y+z=10+w albo y+z+1=10+w. Jedynie y+s=9 było możliwe)
Jawo, nie przypomniałem, a jak widać chyba powinienem, że liczby nie mogą zaczynać się od zera.
mp
Zworka ma też swoje własne znaczenie: http://pl.wikipedia.org/wiki/Zworka
Pierwszy kryptarytm rzeczywiście łatwy (po rozpisaniu):
39270 : 2 = 19635
Nad drugim jeszcze posiedzę
Pierwsze proste: 39270:2=19635
Do jednego rozwiazania „zworki” dochodzi sie szybko przy odrobinie szczescia.
Wystarczy zauwazyc ze Z nie może być rowne 0,1,2,3. Podstawiamy wiec nastepne Z=4, a wtedy [W,S]=[1,2] oraz Y=[6,7,8]. Bardzo szybko ustala sie, ze W=1, S=2, Y=7, a dalej leci blyskawicznie: 172469+247069=419538.
A skoro wiadomo, ze to jedyne rozwiazanie, to jest po sprawie.
a
Sprytnie
mp
Po rozwiązaniu kilkunastu przypadków otrzymałem wynik dla Z=4:
1 7 2 4 6 9
2 4 7 0 6 9 +
—————
4 1 9 5 3 8
Podstawiałem kolejne cyfry za Z i rozpatrywałem pary W i S. Kilka założeń pozwalało szybko weryfikować sens rozwiązywania danego przypadku np. „Z” nie może być 0 ani 1, w kolumnie składników nie może być równocześnie 0 i 9, „A” jest cyfrą parzystą czy fakt, że różnym literom odpowiadają różne cyfry.
Znalazłem inne rozwiązanie:
0 6 3 4 5 9
3 4 6 2 5 9 +
————-
4 0 9 7 1 8
172469+247069=419538
Do rozwiązania dojść można np. tak:
Z=W+S+1 (1, bo Z>W)
W+10=Z+Y+(1) (ta 1 w nawiasie wtedy, gdy S+Y>10)
Wstawiając Z do drugiego równania i odejmując od obu stron W otrzymujemy:
S+Y=9
Ponieważ O nie może być równe zero, O=9 i stąd A=8
R=Z+D+(1) (ta 1 wtedy, gdy Ł>K), więc Z=4 albo Z=5 albo Z=6
Z pierwszego równania wynika teraz W=1 i S=2 albo S=3 albo S=4
Skoro W=1, to zerem może być jedynie D
Wystarczy teraz sprawdzić trzy warianty:
Z=4, S=2, Y=7 i R=5 – więc Ł=6 i K=3 czyli prawidłowo
Z=5, S=3, Y=6 i R=6 czyli sprzeczność
Z=6, S=4, Y=5 i R=7 – dla Ł i K zostają cyfry 2 i 3, więc nie wychodzi
Bardzo ładnie – piątka! (oczywiście za sposób dojścia do wyniku, a nie za sam wynik).
mp