Kształt spod łamańca
Brawa dla Karzyma i Antypa za uporanie się z trudnym zadaniem z poprzedniego wpisu, polegającym na ułożeniu ośmiu ołówków (niekoniecznie równej długości) tak, aby każdy dotykał siedmiu pozostałych. Podstawowe rozwiązanie jest jedno: dwie warstwy po 4 ołówki w każdej – trzy zbieżne, czwarty dotykający ich rozbieżnych końców; warstwy są względem siebie obrócone tak, by każdy ołówek z jednej warstwy dotykał każdego w drugiej. W eleganckim symetrycznym układzie wygląda to tak:
Dwa rozwiązania zaproponowane przez Antypa są bliźniacze, choć topologicznie różne, ponieważ w jednym z nich styk pary ołówków jest odcinkiem, a nie punktem.
Antyp wygrał także konkurs z przedpoprzedniego wpisu, polegający na ułożeniu równości z dokładnie czterema różnymi znakami działań, dokładnie dziesięcioma różnym cyframi i wynikiem – liczbą czterocyfrową (ponadto z całkowitym wynikiem dzielenia). W dodatku wygrał niejako w dwóch konkurencjach, natomiast wcześniej w komentarzu… zrezygnował z nagrody. Czy to oznacza także rezygnację z dwóch nagród, przysługujących podwójnemu laureatowi? Obie nagrody – gry Blokus – czekają.
Gwoli formalności wszystkie różne (inna liczba 4-cyfrowa) rozwiązania zabawy:
(7+9)*65-4/2=1038; (3+8)*97-4/2 = 1065; (6+9)*83-0/7=1245
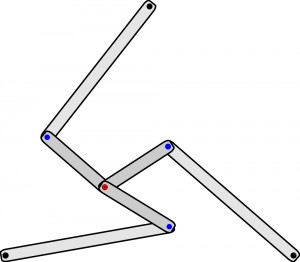
Jeszcze całkiem nie porzucamy ołówków, jeden z nich pojawi się w roli drugoplanowej, natomiast w głównej wystąpią płaskie listewki – trzy długie (równe) i trzy krótkie (też równe). Wszystkie połączone są przegubowo, jak części miarki składanej, zwanej calówką – tworzą łamaniec przedstawiony na rysunku:
Czarne punkty to przeguby nieruchome – miejsca w których łamaniec przytwierdzony jest do podłoża – znajdują się one w wierzchołkach trójkąta równobocznego. Niebieskie przeguby i czerwony to luzaki. W czerwonym umieszczony jest ołówek, który można przesuwać rysując na papierze umieszczonym pod łamańcem, ale oczywiście w ramach obszaru ograniczonego zasięgiem listewek. Proszę możliwie zwięźle i precyzyjnie opisać kształt, który wyznaczają granice tego obszaru. Może ktoś spróbuje określić ten kształt (figurę) dwoma słowami. Zadanie stanowi oczywiście test inteligencji i wyobraźni, więc praktyczne konstruowanie łamańca jest niewskazane, choć bez rysowania zapewne się nie obejdzie.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
Zrezygnowałem z nagrody dlatego, że użyłem programu do rozwiązania zadania. A nie chciałbym mieć „nieczystego” sumienia. Ponieważ kilkoro uczestników konkursu też użyło programu, to mam trochę mniej nieczyste sumienie. Ponieważ mimo udawanej skromności jestem chytry na nagrody to jedną z nagród z radością przyjmę. Drugą nagrodę proponuję przeznaczyć dla Pani albo Pana, którzy nie używali programu do rozwiązania (jeśli Szanowny Gospodarz się zgodzi).
Pozdrowienia
Zgoda!
Los wskazał na Ankę, jako drugą laureatkę (nie ukrywam, że pomogłem losowi, bo podoba mi się „antykomputerowa” wypowiedź Anki).
Adres Antypa powinienem mieć, bo już kiedyś wygrał, ale na wszelki wypadek poproszę o podanie aktualnego na m.penszko@polityka.pl Prośba dotyczy oczywiście także Anki.
m
Patrząc sobie na te krzywki wydaje mi się, że będzie to coś podobnego do trójkąta równobocznego z tym, że z rogami mocno zakrąglonymi a bokami wklęsłymi. Promień wklęsłych boków będzie równy długości dłuższej listewki pomniejszonej o długość krótszej, natomiast promień zaokrąglenia rogów będzie równy długości krótszej.
Jedna połączona przegubowo para listewek o długościach L i l, zamocowana swobodnym końcem dłuższej listewki w wierzchołku trójkąta pozwala na zakreślenie pierścienia kołowego o promieniach R=L+l i r=L-l. Zatem kształtem spod łamańca będzie część wspólna trzech takich pierścieni o środkach w trzech wierzchołkach równobocznego trójkąta.
W przypadku odwrotnym, to jest, gdy swobodne końce krótszych listewek umieścimy w wierzchołkach trójkąta a ołówek zamocujemy w końcach listewek dłuższych, rozwiązaniem będzie część wspólna trzech okręgów o promieniach R.
Pozdrawiam,
Jazz
Niech A,B,C są czarnymi punktami (wierzchołkami trójkąta równobocznego), zaś a,b,c odpowiednimi punktami niebieskimi.
Kiedy punkt X należy do obszaru?
Z nierówności trójkąta muszą być spełnione następujące warunki:
odl(X,a)+odl(A,a)>=odl(A,X)>=odl(A,a)-odl(X,a)
odl(X,b)+odl(B,b)>=odl(B,X)>=odl(B,b)-odl(X,b)
odl(X,c)+odl(C,c)>=odl(C,X)>=odl(C,c)-odl(X,c)
oczywiście odl(X,a)=odl(X,b)=odl(X,c) to długość krótkiej listewki
a odl(A,a)=odl(B,b)=odl(C,c) to długość długiej.
Te warunki wyznaczają nam trzy pierścienie kołowe o promieniu wewnętrznym (długi-krótki) i promieniu zewnętrznym (długi+krótki).
A skoro wszystkie warunki muszą być spełnione, to bierzemy część wspólną pierścieni.
w efekcie wygląda to tak:
http://pokazywarka.pl/51g0zb-2/ (obszar pokolorowany najciemniej)
Dwa słowa to trochę mało, żeby opisać obszar
„Część wspólna trzech pierścieni kołowych” – 5 słów
a jeśli opis ma być ścisły i jednoznaczny,to:
„Część wspólna trzech przystających pierścieni kołowych o środkach w czarnych punktach o promieniu wewnętrznym długości (długi-krótki) i promieniu zewnętrznym długości (długi+krótki)” – trochę więcej słów.
Pozdrawiam
Michał
Poprawię sie troszeczkę po usilnych wpatrywaniach się w łamańca: promień zaokrąglenia rogów będzie żdziebko większy.
Zwięźle chyba mi się nie uda.
Mając do dyspozycji tylko jedno ramię konstrukcji, można narysować pierścień o środku w czarnym punkcie i większym promieniu równym długości dłuższej listewki, a mniejszym równym różnicy długości listewek. Mając trzy ramiona należy znaleźć część wspólną tych obszarów. A to już zależy od proporcji między dłuższą a krótszą listewką.
Tak czy inaczej obszar to część wspólna pierścieni o środkach w wierzchołkach trójkąta równobocznego.
🙂 Przepraszam wszystkich, że moje rozumowanie przebiega na tym forum, ale to z powodu braku czasu i tego, że pracuję 😉 ale moja odpowiedź zaczyna skłaniać się postaci prawie wpisanego sześciokąta z bokami naprzemiennie wklęsłymi i wypukłymi (we wcześniejszych wyobażeniach zapomniałem o trzeciej parze listewek ograniczających ruch w dół).
🙂 I ostatni wpis (nadal wszystko w głowie) wszystko zależy od długości listewek: albo to będzie ‚obły’ trójkąt w środku, albo taki sam ale z ‚wygryzionymi’ rogami.
Mozna zaczac rozwiazywanie zadania od obserwacji, ze niebieskie przeguby tworza okrag o promieniu w czerwonym przegubie. Oznaczmy ramie od czarnego do niebieskiego przegubu poprzez R, a od niebieskiego do czerwonego poprzez r.
Niebieskie linie na ponizszym rysunku pokazuja gdzie sa w stanie dosiegnac niebieskie przeguby, a czerwone obszary oznaczaja miejsca gdzie moze znalezc sie wtedy czerwony srodek. Rozwiazaniem naszego zadania jest czesc wspolna czerwonych obszarow odpowiadajacych kolejnym niebieskim przegubom.
Na przykladowej ilustracji mamy cos przypominajace trojkat rownoboczny o bokach bedacych wycinkami okregu (czy ma to nazwe?)
http://img804.imageshack.us/i/lamiblogaug11.pdf/
Warto zauwazyc, ze (zakladajac elastycznosc przegubow) zadanie ma rozwiazanie, gdy r jest niemniejsze niz odlegosc od okregu o promieniu R i srodku w czarnym przegubie do srodka trojkata wyznaczonego przez czarne przeguby. (Ta odlegosc mozna wyznaczyc patrzac na dwusieczna trojkata o czarnych przegubach).
Gdy proporcje sie zmienia, np R > dlugosc boku trojkata, nasz rysunek bedzie wygladal troche inaczej. Ale otrzymujemy go dokladnie tym samym sposobem.
Kształt zbudowany jest z sześciu łuków. Trzy mają promień równy sumie długości listewki długiej i krótkiej. Ułożone są naprzemiennie z trzema łukami o promieniu równym różnicy długości listewki długiej i krótkiej.
Tak to wygląda http://pokazywarka.pl/lw07dx/
Opisać dwoma słowami – to dopiero sztuka.
Może „wklęsło-wypukły sześciokąt” 🙂
bedzie to wspolny obszar trzech przecinajacych sie pierscieni z srodkami w wierzcholkach trojkata rownobocznego. Ksztaltem przypominajacy szesciokat, ale jego bokami beda luki.
a
Jedna połączona przegubowo para listewek o długościach (dłuższa L i krótsza l) pozwala na zakreślenie pierścienia kołowego o promieniach R=L+l i r=L-l. Zatem kształtem (figurą) spod łamańca będzie część wspólna trzech takich pierścieni o środkach w wierzchołkach trójkąta równobocznego.
Poprzedni mój wpis, przez nieprzemyślany wniosek (ekstrapolację bez uzasadnienia), zawiera błąd.
Pozdrawiam,
Jazz
trójkąt z zaokrąglonymi brzegami? (trójkąt beziera?) Ale coś za łatwo, bo chyba dałoby radę tak dobrać długości patyków, by móc ‚odgryźć’ pewne otoczenie wierzchołków…
Na pewno za to będzie to obszar o 3k osiach symetrii ;). No bo chyba szukanych obszarem nie jest kółko?
Wydaję mi się, że będzie to taki 6 listny „kwiatek”.
Jak widać z komentarzy, odpowiednio dobierając długości listewek można uzyskać kilka ciekawych rozwiązań. Oczekiwałem niecierpliwie na uwolnienie wszystkich komentarzy, gdyż chciałem się zorientować, czy ktoś znajdzie np. takie rozwiązania:
http://pokazywarka.pl/0p4rk7/
Gdy bok trójkąta ma 10 cm, to listewki mają:
– 10 i 6 cm;
– 10 i 5 cm;
– 10 i 4,9 cm.
Warto powiedzieć kilka słów o trzecim rozwiązaniu. Otóż obszar wspólny dla trzech pierścieni składa się z siedmiu rozłącznych części. Zatem mając długości listewek i bok trójkąta jak w przykładzie 3. można zmontować łamańca na siedem różnych sposobów! Ale co ciekawe, każda konstrukcja pozwala na narysowanie jednego podobszaru i nie można przejść z ołówkiem do innych podobszarów. Dlatego dla pewnych długości listewek niepoprawnym jest twierdzenie, że rozwiązaniem jest część wspólna trzech pierścieni.
Pozdrawiam,
Jazz
Jazzie, super! Zagadnienie przeanalizowane dogłębnie dla różnych zależności między długościami promieni i boku trójkata.
m