Przegródki
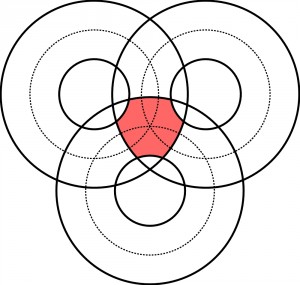
Figura stanowiąca rozwiązanie zadania z poprzedniego wpisu – ślicznie wycyrklowana w kilku komentarzach – wygląda tak (czerwona):
Jej kształt kojarzy mi się z tarczą herbową lub z napierśnikiem (część zbroi). Czy można nazwać ją matematycznie dwoma słowami? Owszem, ale na upartego, bo w polskiej terminologii odpowiednie określenie nie istnieje. Po prostu nie ma potrzeby „chrzcić” tego, co pojawia się sporadycznie jako geometryczny kaprys. Pięciowyrazowe określenie zaproponowane przez Michała: „część wspólna trzech pierścieni kołowych” – ma więc optymalną długość i jest poprawne, choć wymaga doprecyzowania.
W niektórych innych językach mogłoby być jednak krócej. Na przykład dla Anglika lub Amerykanina (matematyka) figura ograniczona łukami okręgów to nie taka rzadkość, więc ma nazwę – wielokąt kołowy (circular polygon), a krzywa zamknięta, stanowiąca jego brzeg określana bywa jako piecewise circular (składana kołowa), czyli odpowiednik łamanej zamkniętej, w której odcinki prostej zastąpione są łukami okręgów. Nie byłoby zatem błędem podpisać figurę na powyższym rysunku: „sześciokąt kołowy” (circular hexagon), choć można by mieć małe wątpliwości, bo boki-łuki wielokątów kołowych są z reguły wypukłe. W polskiej terminologii tylko jeden wielokąt kołowy ma konkretną nazwę – trójkąt Reuleaux, jeśli nie uwzględniać kołowych figur i krzywych, które z wielokątami raczej się nie kojarzą (vesica piscis, arbelos, salinon).
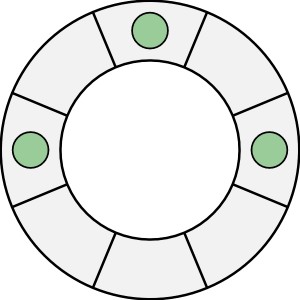
Wróćmy do pierścienia kołowego i podzielmy go na osiem części – przegródek. W trzech przegródkach umieszczamy po jednym żetonie…
… i rozpoczynamy następującą zabawę wielochodową: w każdym ruchu kładziemy w dwóch dowolnych, sąsiednich przegródkach po jednym żetonie. Czy po którymś z kolejnych ruchów może się okazać, że w każdej przegródce będzie tyle samo żetonów?
Oczywiście nie, bo liczba przegródek jest parzysta, a żetonów po każdym ruchu – nieparzysta.
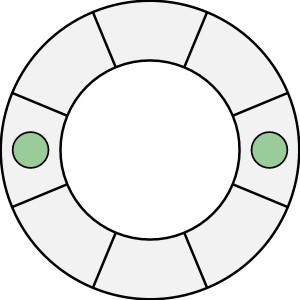
Wobec tego usuwamy jeden żeton:
Zasady ruchów pozostają identyczne, pytanie jest również takie, jak wyżej. A odpowiedź? Jaka by nie była, proszę o jej zwięzłe uzasadnienie.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Nie, ponieważ przerwa między żetonami, mierzona liczbą pól, jest nieparzysta. Nie da rady porozkładać pary żetonów by uzyskać ‚warstę’ o jednakowej wysokości.
Nie, bo na początku suma żetonów na miejscach parzystych jest różna od sumy na miejscach nieparzystych, dowolny ruch nie zmienia tej różnicy, a w rozwiązaniu te sumy są równe.
Niezmienniki się kłaniają.
Na nieparzystych polach mamy 2 żetony, a na parzystych nie ma ich wcale. Po każdym ruchu wzrasta o 1 zarówno łączna liczba żetonów na polach parzystych jak i liczba żetonów na polach nieparzystych. My chcemy, żeby na każdym polu było tyle samo, czyli w szczególności, żeby na polach parzystych było w sumie tyle samo żetonów co na nieparzystych. Jest to oczywiście niemożliwe, bo zawsze na polach nieparzystych będzie o 2 żetony więcej.
A tak poza tematem, to natrafiłem ostatnio na ciekawy filmik związany z tematyką bloga.
http://youtu.be/EO472qM6M9g
Pozdrawiam
Michał
Żetony w ośmiu częściach pierścienia można oznaczyć naprzemiennie dwoma kolorami. Zatem na początku dwa widoczne żetony są tego samego koloru i tym samym liczba żetonów jednego koloru jest większa o dwa od liczby żetonów koloru drugiego. W każdym ruchu zwiększamy o jeden liczbę żetonów każdego koloru. Zatem różnica liczebności żetonów obu kolorów nie zmienia się. Stąd wniosek, że nie można doprowadzić do jednakowej liczby żetonów w każdej części pierścienia.
Pozdrawiam,
Jazz
Niemożliwe jest dołożenie żetonów do równej liczby w każdej przegródce .
Oznaczmy przegródki naprzemiennie jako pola białe i czarne (jak na szachownicy) . Obydwa żetony z pozycji wyjściowej są na polach tego samego koloru . Dokładając żetony na dwa sąsiednie pola jeden trafia na pole czarne a drugi na pole białe . Nigdy nie zrównamy liczby żetonów na polach białych i czarnych , a to jest warunek konieczny (ale nie wystarczający) aby na każdym polu była taka sama liczba żetonów .
Pozdrawiam
AC
To może tak:
Malujemy przegródki na czarno i biało (na zmianę).
W każdym ruchu dodamy 1 żeton do komórki białej i jeden do czarnej.
Ale na początku mamy 2 żetony w (np.) czarnych.
Zatem zawsze w czarnych komórkach będzie o 2 żetony więcej.
Jesli ponumerujemy kolejno pola, to liczba parzystych (p) i nieparzystych (n) bedzie taka sama, a oba poczatkowe zetony znajda sie albo na polach p, albo oba na n.
Nastepne dokladamy zetony tak, ze jeden wpada na pole p, a drugi na n.
Czyli nigdy na polach p nie wypadnie tyle samo zetonow, co na n. Zawsze na jednych bedzie o dwa wiecej lub mniej niz na drugich.
Chyba zwiezle wyjasnilem.
a
Bardziej precyzyjną (choć oczywiście dłuższą) nazwą dla figury z poprzedniego wpisu byłby „wklęsło-wypukły sześciokąt kołowy”.
Nie.
Ponumerujmy przegródki od 1 do 8 (zaczynając od dowolnej) i utwórzmy dwie grupy:
Grupa 1 – żetony w przegródkach o nieparzystych numerach.
Grupa 2 – żetony w przegródkach o parzystych numerach.
Po każdym ruchu zwiększy się o jeden liczba żetonów w obu grupach, więc różnica między liczebnością obu grup jest stała i wynosi 2 – tyle, co w sytuacji początkowej na rysunku.
Malując pola na biało i czarno (na przemian) zaczynając od pola z żetonem, widzimy, że:
1) na białych polach są 2 żetony, a na czarnych nie ma ich wcale
2) dołożenie żetonów na sąsiednich polach zwiększa ilość żetonów na białych i na czarnych polach o 1, zatem na białych zawsze jest o 2 więcej niż na czarnych
3) nie da się uzyskać równowagi między ilością żetonów na białych i na czarnych polach, a to jest warunek konieczny wykonalności zadania.