Kółkokrzyżyki
Kilka wpisów temu przytoczyłem pomysłowe zadanie z czeskiego turnieju sudoku. Kluczem do rozwiązania były umieszczone w niektórych kratkach kółka i krzyżyki.
Kółko było w każdym polu z cyfrą równą liczbie różnych cyfr znajdujących się we wszystkich polach otaczających pole z kółkiem.
Krzyżyk był w każdym polu z cyfrą równą liczbie różnych cyfr znajdujących się w polach stykających się z polem z krzyżykiem tylko rogiem.
W komentarzu Esteon zaproponował, aby zastanowić się nad następującym zagadnieniem: czy można ułożyć zadanie, w którym w jednym lub kilku polach (w ilu maksymalnie?) dałoby się ulokować kółko i krzyżyk równocześnie (nazwijmy takie pola KK)? Z przyjemnością wróciłem do szkółki sudoku.
W KK może być tylko trójka lub czwórka i takie pola mogą się pojawiać wyłącznie w szarych działkach na poniższym diagramie.
Z 16 kratek objętych tymi działkami co najwyżej sześć może być KK, bo w przeciwnym wypadku dwie czwórki lub dwie trójki pojawiłyby się w tym samym rzędzie lub sektorze 3×3. Wszystko wskazuje na to, że sześciu KK także nie da się wcisnąć w diagram, natomiast chyba udałoby się pięć, a cztery – na pewno, co potwierdza poniższy przykład. Uprzedzam, że to twardy orzech, choć do rozwiązania wyłącznie na logikę, czyli bez próbowania i błądzenia. Jankowi Mrozowskiemu (mistrz Polski w sudoku) zabawa zajęła 12 minut. Kto da mniej?


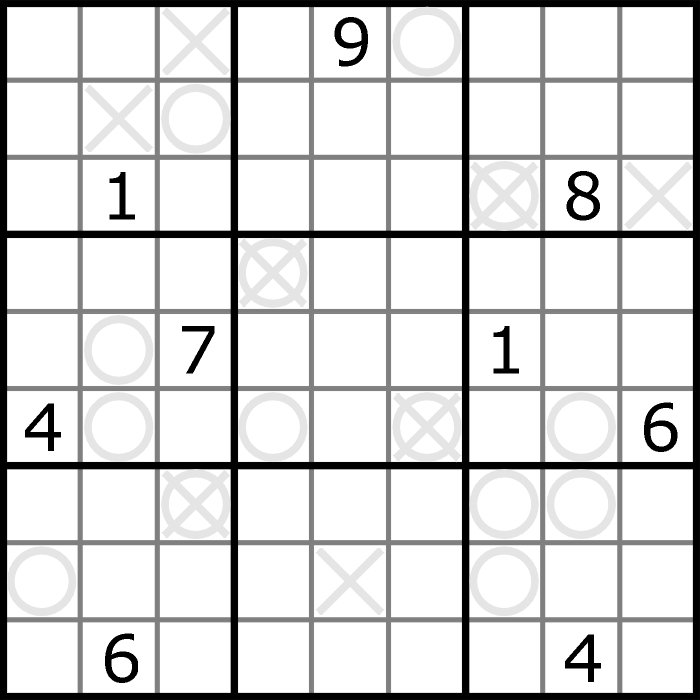

Komentarze
872194635
645238917
913765482
126479853
387652194
459813276
794321568
538946721
261587349
872194635
645238917
913765482
126479853
387652194
459813276
794321568
538946721
261587349
872194635
645238917
913765482
126479853
387652194
459813276
794321568
538946721
261587349
Bardzo trudne i jeszcze bardziej ciekawe. Po prostu super!
Czy jest tajemnica, ile zajelo ulozenie tego diagramu? Ja probowalem ulozyc z 5-cioma przez jakies 2-3h i wreszcie dalem sobie spokoj… I tez nie wierze w istnienie 6 kk w jednym diagramie.
Układałem na raty, w sumie też ok. 3 godzin.
Ale nie żałuję:)
mp