Barierki
Na ile całkowicie różnych sposobów (z dokładnością do odbić i obrotów) można obejść wieżą po trasie zamkniętej diagram n×n, goszcząc tylko raz w każdym polu? Wypada dodać, że jest to możliwe tylko dla parzystych n, więc właściwie chodzi o diagram 2n×2n. Dla n=1 sposób jest oczywiście jeden, dla n=2 – dwa.
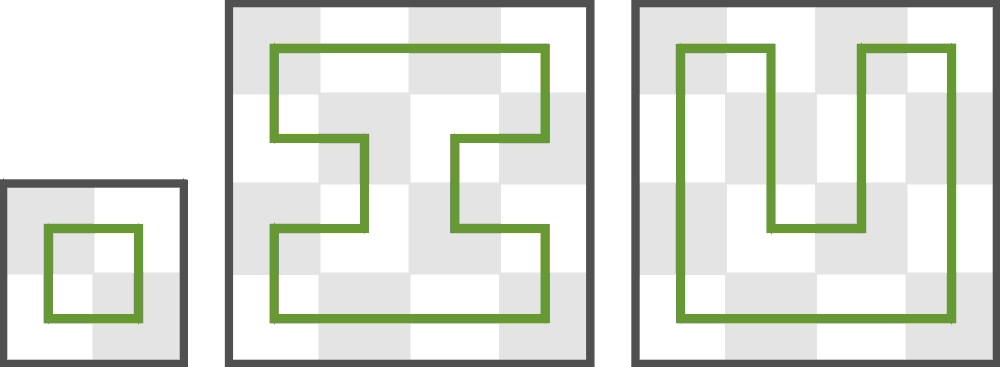
Dalej liczba sposobów bardzo szybko rośnie: dla n=3 jest ich 149, a dla n=4, czyli dla szachownicy – 580717.
Pytanie, które pojawiło się już w Łamiblogu przed wielu laty brzmi: ile co najmniej barier należy ustawić między polami diagramu 2n×2n, aby możliwe było obejście diagramu wieżą tylko w jeden sposób? Pytanie to dotyczyło jednak wówczas konkretnie n=3, czyli diagramu 6×6 (dla n=2 potrzebne są dwie bariery, a ich możliwe ustawienie, zresztą niejedno, łatwo znaleźć). W jednym z komentarzy pojawiło się rozwiązanie z 4 barierami i liczba ta uchodzi dziś za minimalną, choć dowodu, że 3 bariery nie są możliwe – brak.
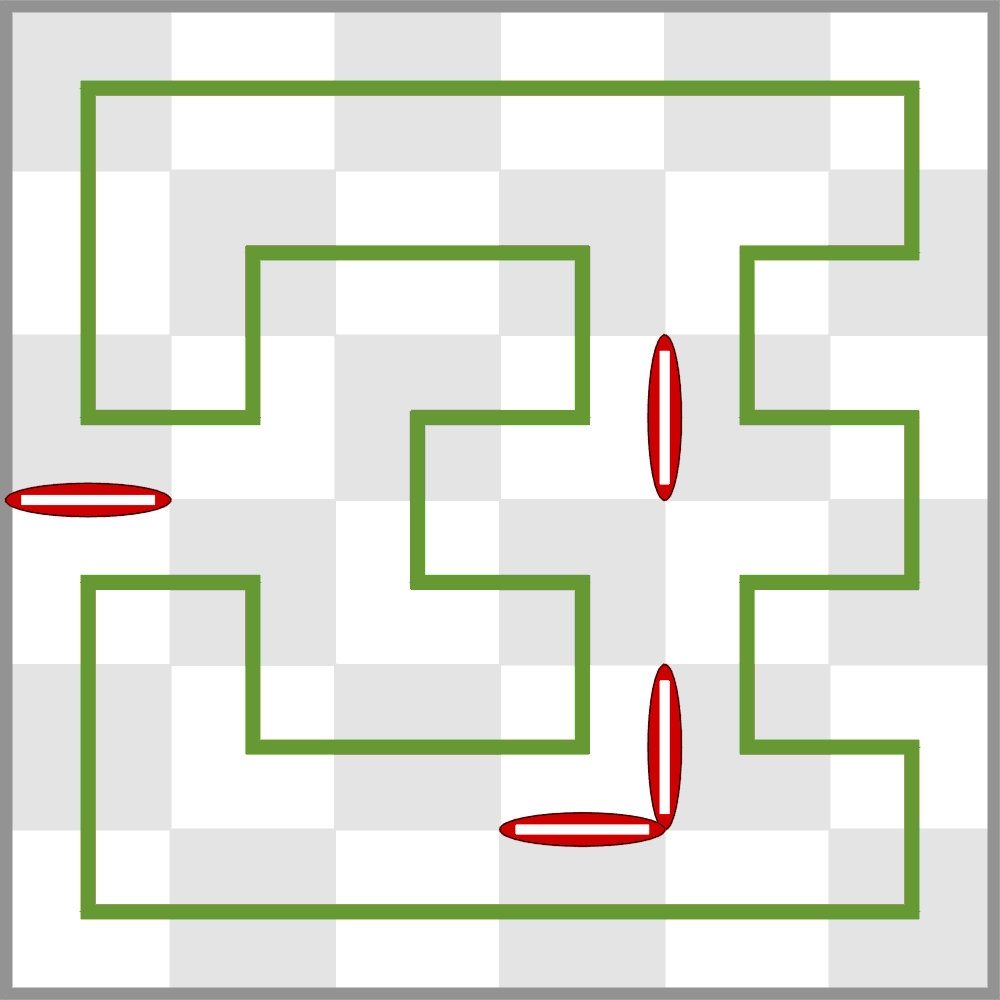
Tym razem analogiczne pytanie dotyczy szachownicy (n=4), więc jest znacznie trudniejsze. Odpowiedzi nie znam i o ile wiem, nikt takiego pytania dotąd nie zadawał. Wstępem do tego tematu może być poniższe zadanie, w którym barier jest aż 16.
Rozwiązanie polega na:
(a) narysowaniu okrężnej trasy wieży, zaliczającej wszystkie pola – każde tylko raz (jako odpowiedź wystarczy podać liczbę załamań trasy na przekątnych diagramu);
(b) próbie usunięcia którejś blokady (blokad) tak, by jedno rozwiązanie było zachowane.
Już (a) jest moim zdaniem nieproste, a (b) – benedyktyńskie, nie wspominając o początkowym pytaniu o minimalną liczbę blokad.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
(a)
Liczba załamań trasy na przekątnych diagramu to 13.
Doświadczony loopowicz zrobi to szybko, ale mniej doświadczeni mogą kluczyć o wiele dłużej.
a) Liczba załamań na przekątnych:
\ : 7 załamań,
/ : 6 załamań.
b) Wygląda na to, że można usunąć barierkę w lewym dolnym rogu (między polem b1 a b2). Założenie, że jej tam nie ma i że trasa wieży przechodzi przez tę krawędź szybko prowadzi do sprzeczności.
Dla wszystkich pozostałych barierek, po ich usunięciu zawsze udawało mi się znaleźć alternatywne rozwiązanie.
Póki co udało mi się znaleźć przykładowy układ 8 barierek, który daje jednoznaczne rozwiązanie (podam je jako pary pól na szachownicy, pomiędzy którymi są barierki:)
a3-a4, c4-c5, e1-f1, d2-e2, g4-g5, f5-g5, h5-h6, c8-d8.
W linku układ 10 barierek.
https://zapodaj.net/plik-wLJ0WfaAWi
Licytujmyż: kto da mniej ?
„nieproste, benedyktyńskie”
Makabra dla zjadaczy łamigłówek. Dopiero co obejrzałem film „Do ostatniej kości” i nie opuszcza mnie pytanie: „Kto zostawi mniej?” Jem regularnie, ale nie zawsze do czysta, a i zdarza się nie napocząć.
a) 13
Zadanie a) nie było wcale trudne. Liczba załamań:
7 na osi Świnoujście-Bieszczady
6 na osi Szklarska Poręba-Suwałki
Zadania b) nie ruszałem:)
b) bez pięciu blokad
Pytanie początkowe: 1
Przepraszam poprawka.
„1” to była odpowiedź na pytanie przedpoczątkowe: „Ile należy aby było niemożliwe”.
Jako ciekawostkę można nadmienić, że rezygnując z zamkniętości drogi otrzymujemy dodatkowo 71 rozwiązań.
https://zapodaj.net/plik-ES5lhCq3vG