Horrendum 2
Kiedy na koncie jest blisko 1200 wpisów w dość wąskim temacie i ma się tzw. swoje lata, to trudno się dziwić, że niekiedy zdarzają się powtórki. Nie takie prawie „słowo w słowo” – choć to też trudno wykluczyć, ale chyba dotąd się nie zdarzyło – lecz dotyczące tego samego rodzaju problemu czy łamigłówki. Bywa też i tak, że świadomie powtarzam jakiś typ zadania, różniący się jednak od prezentowanego poprzednio merytorycznym szczegółem albo stopniem trudności. Tak jest właśnie tym razem i jak wynika z tytułu nowość stanowi ekstremalny stopień trudności. Zadanie należy do kategorii CDS (cyfry do strzałek), która gościła w serii Łamiblogowych wpisów przed sześciu laty.
Do niektórych pól diagramu 8×8 należy wpisać cyfry z zakresu od 0 do 4 tak, aby w każdym wierszu i w każdej kolumnie znalazło się pięć różnych cyfr – trzy pola w każdym rzędzie pozostaną więc puste. W niebieskich kratkach ze strzałkami cyfry muszą się znaleźć, a każda powinna oznaczać, na ile liczb wskazuje strzałka umieszczona w tej kratce.
W przykładzie mniejsze są: diagram (5×5), zakres cyfr (od 0 do 2) i liczba wolnych pól w każdym rzędzie (2).
Przykład

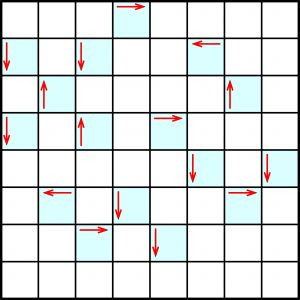
Zadanie pochodzi z kolekcji japońskiego mistrza Inaby Naokiego. Jest bardzo trudne i żmudne – głównie ze względu na występujące w nim sprzężenie zwrotne. Wymaga nie lada uwagi i spostrzegawczości, aby na każdym kroku wypatrywać logicznej ścieżki do celu. Zagadką pozostaje, czy wymaga także w niewielkim stopniu korzystania z metody prób i błędów (ja odrobinę korzystałem, ale być może z powodu nieuwagi i lenistwa). Jako rozwiązanie końcowe wystarczy podać sumę cyfr (ściślej: jednocyfrowych liczb) na przekątnych diagramu.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Czy strzałka może wskazywać poza diagram? Tzn. czy na przykład w górnym wierszu może być strzałka wskazująca do góry (oczywiście z zerem)?
Powinno to być zabronione ale w tekście zadania takiego warunku nie ma.
Mój poprzedni komentarz to wynik nieporozumienia – myślałem, że przy wpisywanych cyfrach też muszą pojawić się strzałki.
18
Moim zdaniem da się rozwiązać logicznie (choć dla mnie pewnym „obciążeniem” było przyzwyczajenie do klasycznej wersji „cyfr do strzałek”, w której w każdym polu jest cyfra i strzałka).
Pełne rozwiązanie:
1XX3204X
3X4XX210
X0XX3421
23140XXX
X40XX132
41X2X30X
X2301XX4
0X214XX3
18
https://images89.fotosik.pl/614/3eba39ba14e08c9c.jpg
Właśnie się zastanawiam, o ile się pomylę, jeśli dam odpowiedź 16?.
Jak można się domyślić wynik został uzyskany metodami „hybrydowymi”.
Bo łamigłówka jest horrendalna, a wielkie liczby mają swoje prawa – mam nadzieję.
Bardzo fajne zadanie, żadnego zgadywania, po nitce do kłębka:
1 x x 3 2 0 4 x
3 x 4 x x 2 1 0
x 0 x x 3 4 2 1
2 3 1 4 0 x x x
x 4 0 x x 1 3 2
4 1 x 2 x 3 0 x
x 2 3 0 1 x x 4
0 x 2 1 4 x x 3
(1+4+3+3)+(1+4+0+2+0)=18
Suma przekątnych 18.
Na początku trudności nakłaniają do wariantów, na końcu lawina potakiwania zwiastuje happy end.
Najtrudniejsze, jak zawsze, wdrukowanie zasad do głowy.
Dobry wieczór,
program komputerowy (przy sporej pomocy logiki ludzkiej do preprocesingu danych) znalazł rozwiązanie:
==========================
Final solution:
|————————|
| 1 X X 3 2 0 4 X |
| 3 X 4 X X 2 1 0 |
| X 0 X X 3 4 2 1 |
| 2 3 1 4 0 X X X |
| X 4 0 X X 1 3 2 |
| 4 1 X 2 X 3 0 X |
| X 2 3 0 1 X X 4 |
| 0 X 2 1 4 X X 3 |
|————————|
==========================
Suma na przekątnych to: 18
Pozdrawiam,