Horrendum
W lipcowym numerze Świata Nauki jest sudoku zdaniem niektórych horrendalne. Co gorsza mocno nietypowe, choć bez dodatkowych „dziwactw”, zatem niemożliwe do ruszenia żadnym dostępnym w sieci programem. Do czasochłonnego pisania programu nikt ze znajomych rozwiązywaczy się nie pali, a niemal wszyscy zarzucają mi, że „pałka się przegła”; nierzadkie są nawet opinie, że nie ma rozwiązania. W tej sytuacji postanowiłem zawczasu przetestować na Łamiblogowiczach domniemaną ekstremalność tego zadania.
Oto diagram.
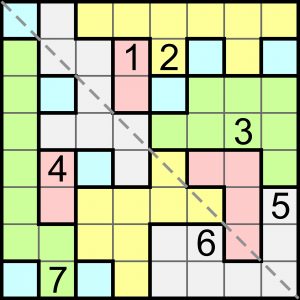
Sudoku jest, jak widać, 8×8 i nieregularne, ale z pewną nietypową nieregularnością: różne cyfry od 1 do 8 powinny znaleźć się w każdym wierszu, w każdej kolumnie, w każdym wydzielonym 8-kratkowym wielokącie, na oznaczonej przekątnej, a także w tercecie różowych wielokątów oraz w oktecie błękitnych kratek.
W rozwiązaniu wystarczy podać sumę cyfr na nieoznaczonej przekątnej, ale oczywiście pełne rozwiązania będą mile widziane – o ile takowe się pojawią.
Ponieważ zadanie jest konkursowe do końca lipca, więc do tego czasu rozwiązań, które być może się pojawią, nie będę ujawniał.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Rozwiązanie:
72163458
86512374
68351247
21748536
34285761
43876125
15427683
57634812
Zadanie jest rzeczywiście trudne, na przykład w porównaniu z https://penszko.blog.polityka.pl/2020/10/31/precz-z-cyframi/ – tam ILP znajduje rozwiązanie w sekundę, tutaj potrzebowało ośmiu minut.
No ale jak się to zapisało na bitach, a nie na liczbach całkowitych, to ILP znajduje rozwiązanie w 0,14 sekundy, tylko czytelność kodu na tym cierpi.
Pełny diagram:
7 2 1 6 3 4 5 8
8 6 5 1 2 3 7 4
6 8 3 5 1 2 4 7
2 1 7 4 8 5 3 6
3 4 2 8 5 7 6 1
4 3 8 7 6 1 2 5
1 5 4 2 7 6 8 3
5 7 6 3 4 8 1 2
Suma na drugiej przekątnej: 51
Do najprostszych zdecydowanie nie należy, ale nie powiedziałbym, że jest też ekstremalnie trudne. Udało mi się je zrobić tylko na logikę, bez zgadywania i bez komputera.
https://images92.fotosik.pl/609/05ac10ffd6175a60.jpg
72163458
86512374
68351247
21748536
34285761
43876125
15427683
57634812
Owszem, „pałka się przegła”, ale nie dlatego, że zadanie jest trudne, ale mówienie o nim, że jest trudne.
Zadanie „wciągnąłem” na jednym oddechu.
(Taki oddech, to praktycznie długi bezdech. Znakomite kwalifikacje na poławiacza pereł. mp)
Jeśli ktoś szuka ekstremalności, to niech spróbuje rozwiązać, z tego samego numeru „Świata Nauki”, diagram z rys. 2c.
Ileż ja się namordowałem przy tym zadaniu, to tylko ja wiem. Wprawdzie na raty, ale w końcu dotarłem do celu.
Rozwiązanie zadania z wpisu: 51.
Odpowiedzi do zadania z rys.2c (lipcowy „Świat Nauki”) nie podam, ze względu na ewentualnych zwolenników masochistycznych doznań pragnących zmierzyć się z tym zadaniem.
Ręcznie dość łatwo („po sznurku”) znalazłem około 17 cyfr i potem chyba trzeba by zacząć poważniej rozgałęziać – za czym nie przepadam.
W tzw. międzyczasie nakarmiłem tymi znaleziskami mój stary program o roboczej nazwie „Moje Małe Monte Carlo” i on wyrzucił coś takiego:
72163458
86512374
68351247
21748536
34285761
43876125
15427683
57634812
Generalnie podsumuję tak:
W mojej ocenie pałka jest do połowy przegnięta.
Suma cyfr z nieoznaczonej przekątnej to 51.
Pełne rozwiązanie:
7,2,1,6,3,4,5,8
8,6,5,1,2,3,7,4
6,8,3,5,1,2,4,7
2,1,7,4,8,5,3,6
3,4,2,8,5,7,6,1
4,3,8,7,6,1,2,5
1,5,4,2,7,6,8,3
5,7,6,3,4,8,1,2.
Zadanie jest trudne, ale można je rozwiązać,
dużo zgadywania, trochę szczęścia ,35 minut
72163458
86512374
68351247
21748536
34285761
43876125
15427683
57634812
Suma przekątnej 51
72163458
86512374
68351247
21748536
34285761
43876125
15427683
57634812
Rozwiązanie jest rzeczywiście jedno (bez warunku różnych cyfr na przekątnej są jeszcze 42 inne) ale faktycznie trudno do niego dojść. „Na logikę” daje się wpisać tylko wszystkie cyfry 7 i trzy cyfry 2. Dalej to już chyba tylko metoda prób i błędów.
Pełne rozwiązanie:
72163458
86512374
68351247
21748536
34285761
43876125
15427683
57634812
Mi wyszło tak, bez prób i błędów tym razem:
Suma na przekątnej: 51
Jedyne poprawne rozwiązanie to:
Modyfikacja istniejących algorytmów jest dość trywialna, np. tej zwięzłej implementacji algorytmu X Knutha: https://www.cs.mcgill.ca/~aassaf9/python/algorithm_x.html
7_2_1_6_3_4_5_8
8_6_5_1_2_3_7_4
6_8_3_5_1_2_4_7
2_1_7_4_8_5_3_6
3_4_2_8_5_7_6_1
4_3_8_7_6_1_2_5
1_5_4_2_7_6_8_3
5_7_6_3_4_8_1_2
@marketaxon
„Algorytm X” to niesamowity algorytm – wielkie dzięki za tę podpowiedź. Wiedziałem że istnieje coś takiego jak exact cover, ale nigdy się w to nie zagłębiłem i używałem backtrackingu.
Przerobiłem implementację, którą podlinkowałeś, tak, aby znalazł rozwiązanie zadania 1 z lipcowego ŚN (chodzi o diagram z rys. 2c, o którym pisze @Andrzej111 – nie podaję tego rozwiązania, bo jeszcze trwa lipiec). Skrypt wykonał się w… sekundę. Nie pamiętam, kiedy ostatnio jakiś algorytm zrobił na mnie takie wrażenie…
Trochę chyba przesadziłeś oceniając, że przerobienie jest trywialne. Zrozumienie, jak dokładnie działa ten skrypt i generalnie na czym polega exact cover, zajęło mi godzinkę z hakiem.
@marketaxon
Również dziękuję za wzmiankę o algorytmie X – szybkość działania piorunująca, zwłaszcza w porównania do bardziej topornych algorytmów.