Heks-lotto
Łamiblog bywa poligonem doświadczalnym dla nowych, choć w różnym stopniu oryginalnych zadań, nim wypłyną one na szersze wody, np. zanim trafią na łamy „Omnibusa”. Tak właśnie jest tym razem. Doświadczalność sprowadza się oczywiście do opinii rozwiązujących.
Zadanie polega na oznaczeniu niektórych sześciokątnych pól z cyframi, czyli np. otoczeniu cyfry kółkiem lub zaszarzeniu komórki. Trzeba to zrobić tak, aby spełnione były dwa warunki:
1) jeśli komórka pozostanie nieoznaczona, to znajdująca się w niej liczba powinna być równa liczbie stykających się z tą komórką pól oznaczonych.
2) jeśli komórka zostanie oznaczona, to znajdująca się w niej liczba powinna być o jeden większa od liczby stykających się z tą komórką pól oznaczonych.
Przykład:

Zadanie:
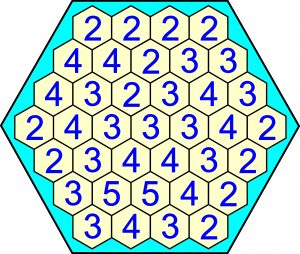
W rozwiązaniu wystarczy podać sumę liczb w nieoznaczonych komórkach. A w ramach doświadczalnictwa proszę o opinię dotyczącą stopnia trudności, a ściślej: czy zadanie nie jest zbyt mozolne ze względu na zakręcone reguły oraz spory udział związanej ze „sprzężeniem zwrotnym” metody prób i błędów?

Komentarze
Pierwsze wrażenie jest (ponoć) najważniejsze:
A dlaczego w zadaniu nie ma żadnej siódemki.
Albo chociaż zera?
Przykład poszedł gładko, właśnie dzięki temu zeru.
A w tym zadaniu jestem na etapie: „mamy dwie piątki – czyli tylko cztery możliwości ich oznaczenia…”- a to wydaje mi się za dużo jak na początek rozwiązywania zadania.
Suma liczb w nieoznaczonych polach wynosi 51.
Zadanie właściwie w całości rozwiązałem metodą prób i błędów (poprzez zaznaczenie lub odznaczenie jednego pola i dochodzenie do sprzeczności) i dość szybko znalazłem rozwiązanie (udało się zgadnąć :D), ale sprawdziłem jeszcze wszystkie inne warianty żeby upewnić się, że rozwiązanie jest jedno. Mimo wszystko, zadanie rozwiązywało się całkiem przyjemnie.
Rozwiązanie to 51.
Drugie wrażenie (po rozwiązaniu):
Zadanie nie jest mozolne – po oznaczeniu dwóch/trzech pól kolejne były już tylko formalnością.
Trudnością było wystartować w miarę niemozolnie (piątki nie sprawdziły się jako dobre miejsce).
Później ewentualnym problemem może być uniknięcie pomyłki o którą jest tu łatwo.
Ogólnie pozostało mi wrażenie, że 90% zadania to był (niestety) automat.
onnn
onooo
oonnno
onnnono
noooon
nonnn
oooo
51
Suma 42. Pełne rozwiązanie:
(2)222
(4)4(2)(3)(3)
(4)(3)234(3)
(2)433(3)4(2)
2(3)(4)(4)(3)2
3(5)542
(3)(4)(3)(2)
Metoda prób i błędów. Ścieżka, sprzeczność, zawracanie; ścieżka, sprzeczność, zawracanie… No trochę męczące to było, trzeba przyznać.
Dobre rozwiązanie. Niedobra suma.
mp
51
Rozwiązanie znalazłem w dziewiątym z kolei wariancie. Trochę za dużo…
Dwie reguły można uprościć do jednej:
Liczba w komórce oznacza liczbę oznaczonych pól w promieniu jednego pola od tej komórki.
Suma liczb w nieoznaczonych polach: 51
Gdyby to zadanie znalazło się w którymś z poprzednich „Omnibusów”, to uznałbym je za jedno z najłatwiejszych do rozwiązania.
Jeśli się nie pomyliłam w dodawaniu (always a challenge), to 51.
Zadanie wydawało mi się łatwe, pierwszą komórkę znalazłam w około pięć minut, a potem już jedna za drugą z górki. W zasadzie zadanie polega na odkryciu pierwszej komórki. I nie na ślepo.
Odpowiedź 51: https://app.box.com/s/dt07olbzzygpr9fyg37oega21d4jvat3
Moim zdaniem ciekawe zadanie, na pewno nie mozolne – trochę podobne do sapera z Windowsa. Na logikę trudno coś posunąć do przodu – ale metodą prób i błędów robi się dość szybko – ścieżki do sprzeczności są krótkie.
Pozdrawiam,
/Tomasz
Wydaje mi się, że najtrudniejszą częścią zadania będzie zsumowanie liczb w nieoznaczonych komórkach. Napisałem „będzie” czyli użyłem czasu przyszłego, bo jeszcze tego nie zrobiłem i raczej nie będzie mi się chciało tego zrobić.
Samo zadanie bardzo trudne nie jest. Moim zdaniem najlepiej zacząć od pary czwórek na brzegu po lewej stronie u góry. Założenie, że któraś z nich jest biała szybko prowadzi do sprzeczności. Do sprzeczności prowadzi też założenie, że biała jest sąsiadująca z nimi trójka. Dalej nic już chyba nie trzeba zakładać – kolejne pola same się ujawniają przy rozwiązywaniu „warstwami” równoległymi do paska z dwiema czwórkami.
Metodą prób i błędów ustaliłem, że oznaczone muszą być dwie czwórki na lewym górnym boku i przylegająca do nich trójka oraz czwórka na dole. Reszta idzie z automatu. Ciekawe czy spójność jednego ze zbiorów i niespójność drugiego to przypadek czy mus ?
https://zapodaj.net/0e2a810cc504a.jpg.html
@Spytko z Melsztyna
Przykładowe rozwiązanie w treści zadania pokazuje, że spójność/niespójność nie jest obowiązkowa.
Układ zaznaczonych pól może być dowolny i to on determinuje ich opis cyfrowy.
@ apartado
Rzeczywiście, w przykładowym zadaniu umknęła mi ta jedynka, która psuje hipotezę 🙂 A to o czym piszesz w następnym zdaniu też mi później wpadło do głowy i to oczywiście wyklucza jakiekolwiek inne „prawidłowości”.
Po chwili namysłu można napisać równanie diofantyczne 4*r+5*s+7*w=113, gdzie:
r to ilość oznaczonych pól narożnych (maksymalnie 6)
s to ilość oznaczonych pól środkowych boków (maksymalnie 12)
w to ilość oznaczonych pól wewnętrznych (maksymalnie 19)
113 to suma liczb wdiagramie.
Komputer wyrzuca 13 możliwych kombinacji:
(#,r,s,w,r+s+w)
1 0 3 14 17
2 0 10 9 19
3 1 5 12 18
4 1 12 7 20
5 2 0 15 17
6 2 7 10 19
7 3 2 13 18
8 3 9 8 20
9 4 4 11 19
10 4 11 6 21
11 5 6 9 20
12 6 1 12 19
13 6 8 7 21
Nasze rozwiązanie figuruje na pozycji nr 11. Teraz komputer wyłowi je w kilka sekund.
@Spytko z Melsztyna
Chciałem wygenerować możliwe wartości (r,s,w) dla pól NIEoznaczonych.
W równaniu zamiast kolejnych 4,5,7 użyłem 3,4,6.
Spodziewałem się, że tym sposobem uzyskam układ „dopełniający” układ dla pól oznaczonych – wskazujący jednoznacznie na jakiś konkretny układ bez konieczności dalszego ich sprawdzania.
Niestety dla wartości 113 uzyskałem taki wydruk:
(#,r,s,w,r+s+w)
1 1 2 17 20
2 1 5 15 21
3 1 8 13 22
4 1 11 11 23
5 3 2 16 21
6 3 5 14 22
7 3 8 12 23
8 3 11 10 24
9 5 2 15 22
10 5 5 13 23
11 5 8 11 24
12 5 11 9 25
„Niestety” bo wśród tych możliwości nie ma układu, który dopełniałby rozwiązanie dla pól oznaczonych czyli r=5,s=6,w=9.
Dopełnienie (polami nieoznaczonymi) powinno być r=1,s=6,w=10.
Żeby było bardziej zagadkowo dodam, że układ pól nieoznaczonych r=1,s=6,w=10 można uzyskać dla sumy 87 (zamiast 113).
Poniżej możliwe kombinacje.
Układ „dopełniający” jest na pozycji 3.
(#,r,s,w,r+s+w)
1 1 0 14 15
2 1 3 12 16
3 1 6 10 17
4 1 9 8 18
5 1 12 6 19
6 3 0 13 16
7 3 3 11 17
8 3 6 9 18
9 3 9 7 19
10 3 12 5 20
11 5 0 12 17
12 5 3 10 18
13 5 6 8 19
14 5 9 6 20
15 5 12 4 21
To 87 uzyskałem sprawdzając kolejne wartości i nie wiem dlaczego zadziałało właśnie 87.
Czy mógłbym uzyskać jakąś wskazówkę?
@apartado
Zmniejszenie współczynników równania to zmiana sposobu liczenia wartości w diagramie i prowadzi do innego zadania a nie do liczenia zbiorów dopełniających. To, że dla 87 wychodzi to przypadek. Tak naprawdę metoda równania diofantycznego to straszne marnowanie informacji bo przecież można ułożyć układ 37 równań z 37 niewiadomymi i dokładnie wyliczyć gdzie są jedynki a gdzie zera 🙂
@apartado
Zadałem sobie trud rozwiązania tego układu programem i okazało się że układ ma 4 równania zależne. Po ustaleniu 4 zmiennych, tak jak przy ręcznej robocie, resztę już policzył dobrze.
@apartado
Wg mnie nie możesz tak po prostu zamienić współczynników – w równaniu dla pól oznaczonych liczymy ile razy dane pole jest liczone, dla nieoznaczonych nie miałoby to sensu.
Jeśli chcielibyśmy równanie dla nieoznaczonych to powinniśmy zrobić tak:
4*(6-r) + 5*(12-s) + 7*(19-w)=113
co po przekształceniu daje
4*r+5*s+7*w=104
i trójka 1,6,10 spełnia to równanie.
Dziękuję za wyjaśnienia.
Obok tego „104” też „przechodziłem” 😉
@problem „104”
Poniżej plansze dla odwróconych zbiorów (oznaczone / nieoznaczone). Suma pól – 104.
https://zapodaj.net/535e211a01573.jpg.html