Konik na kamieniach
Dziś będzie zadanie, które wymyśliłem 40 lat temu i chyba gdzieś je dawno temu opublikowałem. Jest ono przejawem dwu „chorób”, którymi zaraziłem się w dzieciństwie i pewnie już nigdy się z nich nie wyleczę – domino-28 i szachy-64. Obie raczej nie są zakaźne, ani zbyt dotkliwe, więc z czystym sumieniem pozwalam sobie na reaktywację.
Z kompletu domina wybieramy wszystkie, czyli siedem kamieni z „mydłami” (połówkami bez liczb-oczek) i układamy z nich taki oto wielobok:
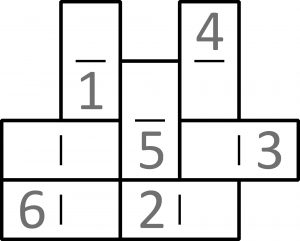
Jeśli ten układ potraktujemy jak kawałek szachownicy, której polami są połówki kamieni, to możliwe będzie obejście go ruchem skoczka szachowego w następującej kolejności: najpierw konik obskakuje wszystkie osiem mydeł, a potem liczby kolejno od 1 do 6. Cała trasa wygląda tak:
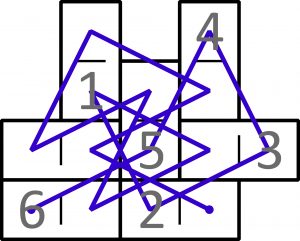
Zadanie polega na ułożeniu z tych samych siedmiu kamieni prostokąta 3×5 bez rogu:
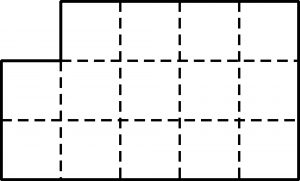
Wyszczerbiony prostokąt powinien być tak ułożony, aby konik mógł obskoczyć go jednym ciągiem dokładnie w taki sam sposób jak poprzednio – najpierw wszystkie zera-mydła, potem od 1 do 6.
Jako rozwiązanie wystarczy podać trzy rzędy cyfr – podział (a właściwie podziały) na kamienie oraz trasa będą wówczas łatwe do odtworzenia. Jednak ustalić rozmieszczenie cyfr nie jest łatwo.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
0300
60014
02500
_ H 3 B E
4 C F 1 6
G 2 5 D A
Litery to mydła. Trasa prowadzi tak:
A-B-C-D-E-F-G-H-1-2-3-4-5-6
https://www.fotosik.pl/zdjecie/ab0e5081b6357a92
To zadanie nie ma tylko jednego rozwiązania. Przykładowe rozwiązanie:
XH3DA
4CF16
G25BE
A..H kolejne skoki po „mydłach”, zaczynając od prawego górnego rogu.
1..6 skoki po liczbach. Można zmieniać układ kamieni.
Dobry wieczór,
Znalazłem dwa rozwiązania (a właściwie 2x2x2 = 8) i nie było bardzo trudno 😉
Rzędami:
0300/40016/02500
0300/60014/02500
Rozwiazanie rysunkowe tu:
https://app.box.com/s/1ul3k2pj7zmnv332ixpir9q1ev6ujbae
Pozdrawiam i życzę zdrowia 😀
PS. Są jeszcze dwie inne ścieżki skakania – ale układ kamieni się nie zmienia.
x0300
60014
02500
trasa od 01 d0 14
,x,08,11,02,05
14,03,06,09,12
07,10,13,04,01.
0300
60014
02500
Pola ponumerowane według kolejności odwiedzania:
X,8,11,4,1
12,3,6,9,14
7,10,13,2,5
X – wyszczerbienie prostokąta.
_0300
40016
02500
https://s6.ifotos.pl/img/Konikjpg_qqnqsrp.jpg
Widzę nieistotny dual.
Przyznam się że nie bardzo rozumiem jak podać rozwiązanie, ale spróbuję na swój sposób.
O = „mydło”
Pierwszy rząd – dwa kamienie poziomo:
O3 OO
Dwa następne rzędy – wszystkie kamienie pionowo
4 O O 1 6
O 2 5 O O
Kolejność skoków od 1 do 14 rzędami:
8, 11, 2, 5
12, 3, 6, 9, 14
7, 10, 13, 4, 1
Pozdrawiam wszystkich serdecznie!
No i bardzo ładnie Pani Baśu 🙂
mp
7, 4, 13 ,10
1, 12, 9, 6, 3
8, 5, 2, 11, 14
Coś tu nie gra.
mp
W „Omnibusie wakacyjnym” z tego roku jest kilka zadań o nazwie „Zaułki”.
Ostatnie zadanie z tej serii nie ma rozwiązania. Rozwiązanie podane w „Omnibusie” jest złe. Proszę zwrócić uwagę na prawy górny róg. W rozwiązaniu są cztery białe kratki, a zgodnie z regułami nigdzie nie może by kwadratu 2×2.
Aby było jedno rozwiązanie, należy rozbić leżące w tym rogu tetromino na dwie części złożone z jednej i trzech kratek (trzy kratki są poniżej jednej).
Zgadza się, tzn. jest byk; no – byczek.
mp
Co nie gra? Układ domina jest następujący:
1szy rząd (poziomo): (m, 4) (m, m)
2gi i 3ci (pionowo – tzn. 2gi element poniżej) (1,m) (m,5) (m,2)(6,m)(3,m)
Skoki: m(3)->lewe m(m,m) ->m(5)->m(6)->prawe m(m,m)->m(2)->m(1)->m(4)->6->5->4->3->2->1
Drobiazg. Konik skacze po cyfrach od 6 do 1, a powinien odwrotnie.
mp
LOL. To skrót myślowy. Bez znaczenia…
Ajcar
mp
Cztery drogi konika, kamiennych plansz więcej, dwa ustawienia cyfr.
Sumy w rzędach: 3,11,7.
Sumy 7,5,9 (9,5,7) nie z domina. Skakać można ale miękko – bez kości.
Jest 8 różnych dróg które wpisują się w 2 różne podziały pól między mydła (0) i cyfry (1,2,3,4,5,6).
Niestety (albo na szczęście) jeden z tych schematów nie daje się podzielić na domina gdyż zawsze wychodzą dwa kamienie z podwójnym mydłem.
Co ciekawe w obu tych schematach układy pól stałych i zmiennych są takie same.
Podsumowując, jeśli nie rozróżniamy mydeł ale rozróżniamy pola z cyframi to mamy DWA rozwiązania:
XH3DA
4CF16
G25BE
Drugie rozwiązanie otrzymujemy zamieniając 4 i 6.
Jeśli rozróżnialibyśmy mydła to zamienić można DA z BE co razem daje 2*2=4 różne drogi.
Ten drugi schemat drogi (nierozbijalny na kamienie domina) wygląda tak:
XGD36
A41FC
HEB52
Tu możemy zamienić dokładnie te same (geometrycznie) układy pól co w pierwszym schemacie czyli:
A z C oraz
36 z 52
Łatwo sprawdzić, że podział na domina jest tu niemożliwy.
Dość prosta, acz ładna analiza
mp