Policja na działkach
Dopadła mnie słowacka policja. Jechałem sobie grzecznie rowerem do Popradu, a oni cap! – i już mnie mają. Wiem, że to mało łamigłówkowy temat, ale ponieważ blogu dla cyklistów na portalu Polityki nie ma, więc pozwalam sobie wcisnąć parę słów ku przestrodze, może się pocztą pantoflową rozniesie i komuś przyda.
Jeżdżę bez kasku i dotychczas nikt mi z tego powodu na drodze nie stawał. Nie wiedziałem niestety, że mniej więcej od jesieni 2008 roku kask na Słowacji jest obowiązkowy dla wszystkich pedałujących poza miastami, a dla dzieci do lat 15 także w miastach. Dopiero teraz poinformowali mnie o tym policjanci, a także ujawnili w sekrecie 🙂 , że dotąd na niesubordynowanych cyklistów patrzyli przez palce, natomiast w tym roku dostali prikaz, aby się za takich jak ja ostro wziąć. Póki co zostałem pouczony, ale wszystkich, którzy zamierzają w te wakacje jeździć rowerem po Słowacji bez kasku uprzedzam, że warto mieć przy sobie 30 euro – tyle kosztuje u naszych sąsiadów brak skorupy na głowie.
A teraz do rzeczy.
Zadanie z poprzedniego wpisu można by zaliczyć do geometrii rekreacyjnej. Formalnie takiego określenia nie ma, jest tylko matematyka rekreacyjna, ale mniej więcej jej połowę stanowi „jazda figurowa”. Ta z kolei obejmuje różne rodzaje zadań, a wśród nich do klasyki należą te, w których figury są cięte. Dawniej zabawa polegała zwykle na takim rozcinaniu, aby kawałki miały jednakowy kształt i wielkość albo by można było z nich złożyć inną figurę. Obecnie dominują parcelacje prostokątnych pokratkowanych włości na wielokątne działki – zgodnie z jakimiś regułami. Dlatego wspomniane zadanie z Wędrowca sprzed ponad 100 lat jakby wyprzedziło swoje czasy. Nie przypominam sobie nic podobnego XIX-wiecznego.
Natomiast doskonale pamiętam przynajmniej kilkanaście takich typów zadań z przełomu XX i XXI wieku, powstałych głównie w ojczyźnie sumo i sushi. Część z nich jest nadal w modzie, a najciekawsze wprosiły się do paru kolejnych wpisów łamiblogowych w ramach cyklu „czy mnie jeszcze pamiętasz?”.
Zacznę od shikaku, które dawniej nazywałem działkami, ale od kiedy japoński stał się międzynarodowym językiem główkołamaczy, złamałem się i zdradziłem polszczyznę.
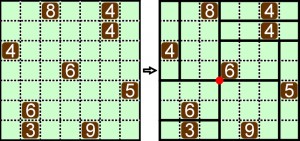
Zasady są uroczo zwięzłe i proste: diagram należy podzielić wzdłuż przerywanych linii na prostokątne działki tak, aby w każdej znalazła się jedna liczba – równa liczbie kratek tworzących tę działkę.
Przykład:
Ogólnie rzecz biorąc, zadania są logicznie klarowne. Sprowadzają się do wyciągania jednoznacznych wniosków z alternatywnych układów prostokątów. Nierzadko trafiają się pewniaki, czyli alternatywy nie ma. Poniższe zadanie należy do średnio trudnych (?).
Proszę wskazać miejsce, od którego można zacząć parcelację, lokując w nim prostokąt-pewniak. A może takich miejsc jest kilka? Jako rozwiązanie końcowe wystarczy podać, w ilu miejscach krzyżują się linie podziału (w przykładzie w jednym – czerwona kropka).
Wypada dodać, że shikaku powstało w fabryczce Nikoli, a debiutowało w roku 1991.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
Super. rozwiązywałem już takie wcześniej, ale to jest jakieś takie inne, świeże. Pewnie dlatego, że jest hand-made, a nie computer-generated. Jeśli się nie mylę, to (….. cenzurka tymczasowa) styku czterech działek – działki te mają pola (……).
Pozdrawiam!
Linie podziału krzyżują się w jednym miejscu. Jednoznaczne jest położenie kwadratu o polu 4 w lewym górnym rogu oraz prostokąta o polu 8. Dalej łatwo.
Ja zacząłem od 4 w lewym górnym rogu, następnie 3 pod nią itd. Linie podziału krzyżują się w jednym miejscu. Działki o polach 3,3,3,6.
Parcelację można rozpocząć od dowolnego miejsca, oczywiście, jeśli jest się przygotowanym do odpowiednio głębokiej analizy typu: jeśli … to … , jeśli…to … , jeśli… to … , itd.
Ja zacząłem od wyznaczenia działki 2×2 w lewym górnym rogu, bo tak było dla mnie najłatwiej.
A teraz, coś dla tych, którzy nie wiedzą, skąd wziąć 30 euro
http://www.multimagie.com/Init.htm
witam, lekkie i przyjemne zadanko. zacząłęm od lewej górnej 4 , poszedłem w dół pierwszą kolumną, a potem się przerzuciłem na prawą skrajną kolumnę od środka do górnego prawego rogu.
Znalazłem tylko jedno miejsce – skrzyżowanie (pomiedzy 5 i 6 rzędem oraz 1 i 2 kolumną)
pozdrawiam
Znalazłem 2 prostokąty-pewniaki: z 4 w lewym górnym rogu i z 3 w ostatniej kolumnie.
Po podziale wyszło mi jedno skrzyżowanie linii podziału (przy działkach o polach 3,6,3,3).
http://img218.imageshack.us/i/84613249.jpg/
Pewniaki to 4 w lewym górnym rogu i 3 w prawym dolnym.
Pewniaki sa dwa – „czworka” przy lewym gornym rogu i trojka u dolu przy prawym brzegu. Skrzyzowanie jest jedno – na styku dzialek 3-3-4-6.
Latwe, ale przyjemne.
a
dziekuje za uratowanie niedzieli
p.s.
co do kaskow zdania sa podzielone:
mniej urazow glowy,ale wiecej kregoslupa.
Oczywistym prostokątem jest 4 w lewym górnym rogu. Po niej od razu oczywista staje się 3 poniżej. A linie podziału krzyżują się tylko w jednym miejscu.
Pozdrawiam.
Pewniaki są co najmniej 2:
– lewy górny róg – pole jest w „zasięgu” tylko jednej cyfry – 4
– 3 czwarta od dołu po prawej -> musi znajdować się przy krawędzi prostokąta ją zawierającego, w przeciwnym przypadku 6 dwie kratki niżej nie ma miejsca na swój prostokąt.
Znak krzyża odnajduję w 1 miejscu.
A oto graficzne przedstawienie rozwiązania:
http://www.tarczynski.info/lamiblog/lamiglowka.jpg
A teraz z innej beczki:
trafiłem na australijską stronę CiSRA i … oniemiałem 🙂 jak zobaczyłem rozwiązanie pierwszego zadania konkursowego z tamtego roku na stronie
http://puzzle.cisra.com.au/2009/puzzles.html
zadanie o nazwie: A.1 Tooth and Claw
Żadne zadanie nie ma instrukcji, trzeba sobie popatrzeć i dać odpowiedź.
Popatrzcie sobie najpierw na zadanie i domyślcie się o co tu chodzi, a potem porównajcie sobie co ONI tam wymyślili.
A tak przy okazji, można sie rejestrować na ten rok, w połowie maja konkurs:) (nie wiem czy polacy mogą, ale to mało ważne, poszperać po starych zadaniach też można).
Skorzystam jeszcze z uprzejmości gospodarza i podziele sie tylko jeszcze jednym linkiem (już sie skończyło, ale zadanka można porozwiązywać):
http://www.turkzeka.com/zeka/pdf_doc_html/TZ_2010e.html