Mnożenie LCD

Łamigłówki z cyframi „elektronicznymi” to właściwie klasyka, choć debiutowały raptem przed niespełna półwieczem wraz z rozpowszechnieniem się kalkulatorów kieszonkowych. Chodzi oczywiście o kreskowe cyfry występujące na 7-segmentowym wyświetlaczu – dawniej diodowym, dziś ciekłokrystalicznym.

Zwykle w zadaniach mowa jest o uszkodzonym displeju, a praktycznie na rysunku znajduje się działanie z niekompletnymi cyframi, które trzeba rozszyfrować. Przykładem może być prosta łamigłówka z ostatniego zimowego Omnibusa:

Bez dodatkowego warunku zadanie ma trzy rozwiązania.
(a) 67×7=469
(b) 68×6=408
(c) 69×7=483
Aby było jedno rozwiązanie, potrzebny jest dodatkowy warunek. Nasuwa się następujący (taki był w Omnibusie):
(I) wszystkie cyfry w mnożeniu powinny być różne.
Wówczas rozwiązaniem jest (c).
Warunek mógłby brzmieć jednak inaczej – tak, aby zadanie było nieco bliższe displejowej rzeczywistości, a mianowicie:
(II) taka sama cyfra zawsze wyświetla się błędnie w taki sam sposób, ale różne cyfry też mogą się błędnie wyświetlać jednakowo.
Zauważmy, że przy warunku (II) jedynym rozwiązaniem również byłoby (c), ponieważ zarówno w (a), jak i w (b) są dwie szóstki, a jedna z nich wyświetla się inaczej niż druga.

Kolej na (za)danie główne, czyli kreskowe mnożenie, które wypadło z przygotowywanego 11. Omnibusa, ponieważ konsultanci uznali je za zbyt trudne (żmudne):

Mnożenie ma jedno rozwiązanie przy warunku (I) i  jedno więcej niż jedno (ile?) przy warunku (II). Czy uda się Państwu znaleźć oba wszystkie?

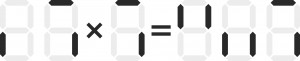
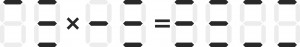
Komentarze

[OlaGM]

(I)
82*45=3690

(II)
69*32=2208
32*69=2208
73*46=3358
73*53=3869
75*48=3600

Pani Olu, czy Pani znalazła te rozwiązania na piechotę? Nie chce mi się wierzyć, bo to jest zajęcie benedyktyńskie, a Pani rozwiązała zaskakująco szybko. Z drugiej strony mam wątpliwości, czy wsparła się Pani komputerem, bo rozwiązań (II) jest więcej. Dlatego proszę o rozwianie moich wątpliwości.
Pozdrawiam
mp

[Jacwing]

Rozwiązanie dla pierwszego warunku:
82 x 45 = 3690

Rozwiązania dla drugiego warunku:
32 x 69 = 2208
69 x 32 = 2208
73 x 46 = 3358
83 x 43 = 3569
75 x 48 = 3600
82 x 45 = 3690
78 x 49 = 3822
73 x 53 = 3869

Jeśli ktoś jest zainteresowany to kod programu znajdzie na https://github.com/Jacwing/MnozenieLCD

[Spytko z Melsztyna]

Warunek I:
82 * 45 = 3690
Warunek II (8 rozwiązań):
32 * 69 = 2208
69 * 32 = 2208
73 * 46 = 3358
73 * 53 = 3869
75 * 48 = 3600
78 * 49 = 3822
82 * 45 = 3690
83 * 43 = 3569
łatwe, siłowe dla komputera 🙂

[OlaGM]

Komputerowo, programem do rozwiązywania kryptarytmów.
Pozdrawiam 🙂

[OlaGM]

(II)
83*43=3569

[aps1968]

Przy warunku I mamy:
82×45=3690
Jest to także oczywiście rozwiązanie przy warunku II. Dodatkowe rozwiązania przy warunku II są takie:
32×69=2208
69×32=2208
73×46=3358
73×53=3869
75×48=3600
78×49=3822
83×43=3569
Jak widać, nie ma rozwiązania idealnego, za które można by uznać wyświetlanie każdej pary różnych cyfr niejednakowo. Wtedy iloczyn musiałby być postaci xxyy.

[timon]

I warunek
82*45=3690
II warunek
32*69=2208
69*32=2208 Jedyna „przemienna” para

73*46=3358
75*48=3600
78*49=3822

82*45=3690
83*43=3569

[jukka2003]

Nie sprawdzalem dokladnie ale moje wyniki to:

Liczba kombinacji (I) = 1
82×45=3690

Liczba kombinacji (II) = 8
32×69=2208
69×32=2208
73×46=3358
73×53=3869
75×48=3600
78×49=3822
82×45=3690
83×43=3569

[Antyp1958]

Rozwiązań z pierwszym warunkiem jest jedno
82×45=3690
Rozwiązań z drugim warunkiem jest pięć
32×69=2208
75×48=3600
78×49=3822
83×43=3569
no i rozwiązanie z pierwszym warunkiem.