Kwadratura zegara
Zadania zegarowe stanowią odrębną i niemałą działkę matematyki rekreacyjnej. Dorzucam do tego ogródka jeszcze jeden kamyczek.
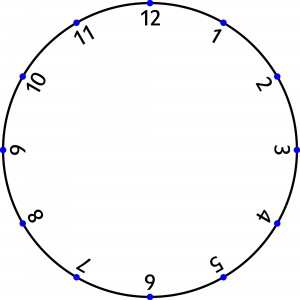
Potraktujmy tarczę zegara jako obiekt geometryczno-liczbowy, czyli okrąg, na którym rozmieszczono w jednakowych odstępach dwanaście punktów oznaczonych kolejno liczbami od 1 do 12.
Na rysunku powinien pojawić się kwadrat umieszczony tak, aby na jego obwodzie znalazło się jak najwięcej punktów godzinowych oraz aby suma liczb, odpowiadających tym punktom, była kwadratem. Które punkty będą wspólne dla okręgu i brzegu kwadratu?

Komentarze
Jeżeli niczego nie przeoczyłem, to wygląda na to, że albo będą do kwadratu należeć 4 punkty, i wtedy suma kwadratem nie chce być, albo 2, a nie 3. Mielibyśmy wtedy takie rozwiązania jak dowolne kwadraty z udziałem par (12, 4), (11,5), (10,6), (9,7). Kwadratu o boku 0 w punkcie 9, co dałoby 36, nie liczę.
1,3,5,7,9,11
P.S. To teraz mam juz konto na Polityce! 🙂
Przepraszam za pomyłkę, spisałem z kartki ale nie to co trzeba.
To jest poprawne:
2,3,4,7,10,11,12
suma 49, pierwiastek to 7
🙂
Na razie znalazłem dwa rozwiązania:
2,4,8,10,12
oraz
1,3,5,7,9
Jeszcze sprawdzam czy da się więcej…
Kwadraty zawierające 8 punktów godzinowych nie chcą być kwadratowe liczbowo, kwadratów z 7 lub 6 punktami nie potrafię narysować, więc obstawiam kwadrat zawierający 1+3+5+7+9 = 25.
5 na stycznej, 1 i 3 oraz 7 i 9 na siecznych, czwarty bok nie zawiera punktów godzinowych (ale gdyby zagiąć cyferblat wzdłuż siecznej zawierającej 10 i 12, to jeszcze 11 by się załapała ;-)).
Udało mi się znaleźć rozwiązanie z 7 punktami wspólnymi: 2, 3, 4, 7, 10, 11, 12
Ich suma to 49.
Rysunek poglądowy: http://www.gg.pl/dysk/QUgkRbgG_0xQQEgkRbgG72U/zegar.png
Poćwiczyłem rysowanie i jednak da się lepiej: 2+3+4+7+10+11+12 = 49.
Sieczne przez pary: (2,3); (4,7); (7,10); (11,12). Czyli siódemka jest jednym z wierzchołków.
nie jestem na 100% pewien czy narysowałem kwadrat, niemniej „na oko” wygląda dobrze, suma to 49
http://bankfotek.pl/view/1812709
Lepiej nie można 🙂
mp
Oczywiście poprzednie moje „rozwiązanie” to było nieuważne przeczytanie, że nie w ogóle na obwodzie, tylko w wierzchołkach… Rzeczywiście największą do pomyślenia liczbą punktów leżących na obwodzie kwadratu jest 8, ale to nie wychodzi. Prowadzimy sieczną przez 11 i 12, potem prostopadłą do niej przez 2 i 3, i potem chciałoby się dojechać do 5 i 6…. ale skręćmy wcześniej, żeby przez 4 i 7, oczywiście 4-7 jest równoległa do 5-6. No ale 1-7 jest symetralną kąta prostego 11-12 z 2-3, skąd wniosek, że 7 musi być wierzchołkiem. A skoro tak, to do boku kwadratu musi należeć także punkt 10, mamy więc 11+12+2+3+4+7+10 = 49. Takich kwadratów da się narysować 12, bo każdy punkt może być wierzchołkiem, ale w żadnym innym przypadku suma nie jest kwadratem. Ciekawe, że akurat pierwsze pomyślane rozwiązanie spełnia warunek, szansa teoretycznie 1:12.
2, 3, 4, 7, 10, 11, 12
11 – 9 – 5
Jeżeli dodamy te trzy liczby dostaniemy 25 (sprawdzone na kalkulatorze).
Znalazłem lepsze rozwiązanie:
(2,3,4,7,10,11,12) = suma 49
Zaskakujące jest jak wiele kwadratów da się powiązać z tarczą zegara 😀
2, 3, 4, 7, 10, 11, 12 🙂
12,11,10,7,4,3,2 = 49
(11+12)+(2+3)+(4)+[7]+(10) = 49
Zupełnie nie na temat, ale pomyślałem, że przedstawię tu swój problem:
jakie jest najefektywniejszy sposób na parowanie skarpetek?
Ostatnio zostałem zarzucony, siedząc spokojnie na fotelu, stertą skarpetek, które po upraniu rzuciła mi żona. Było ich mnóstwo. Siedząc tak i parując je zastanawiałem sie, czy jest jakis sposób na sparowanie ich. Na końcu okazało sie, że zostało mi 5 skarpet bez pary. Na szczęście nie był to mój błąd, suszyły sie w innym miejscu.
Ale problem został… jak sparować skarpety, jeśli jest ich tyle, że rzut oka tu nie pomoże?
Ahoj,
moim zdaniem kwadrat może zawierać maksymalnie 8 punktów (nie umiem narysować boku kwadratu zawierającego trzy punkty). Są wtedy 4 możliwe zestawy liczb, z których żaden nie jest kwadratem. Obniżając nieco loty, możemy narysować kwadrat przez 7 liczb. Jeden z nich (więcej nie szukałem) o wierzchołkach w punktach 4, 7 i 10 oraz bokach przechodzących przez punkty 2 i 3 oraz 11 i 12 sumuje mi się do 49.
No tak, musiałem się pomylić. Wierzchołki w punktach 4 i 10 nie są w samych punktach, tylko nieco poza okręgiem. Zatem finalnie kwadrat ma jeden wierzchołek na okręgu (w punkcie 7), wychodzące z niego boki przechodzą przez 4 i 10, a pozostałe 2 boki odpowiednio przez punkty 2 i 3 oraz 11 i 12.
Blog niepielęgnowany grozi uwiądem.
czy to koniec tego wspaniałego bloga? oby nie…
To tylko przejściowy brak czasu i natchnienia 🙂
mp
wiąz,
Kup z 10 par identycznych skarpetek.