Drabina Jakubowa
Niektórzy z czytelników Łamibloga sympatycznie zareagowali na moją przejściową „dysgrafię komputerową”, nadsyłając propozycje oryginalnych, nieprostych zadań. Oto jedno z nich – autorstwa Pana Janusza Wojtala.
Unia Europejska ogłosiła konkurs, według pomysłu posła Jakubowa, na projekt kosmicznej (teoretycznie nieskończonej) drabiny, która będzie służyła do pieszych wędrówek na dowolne ciało niebieskie we wszechświecie. Aby jednak wspinaczka nie była monotonna, na posiedzeniu Rady Europy uchwalono, że niektóre szczeble z tej drabiny należałoby usunąć – te mianowicie, które są bokami w określonych trójkątach.
Ściślej, chodzi o trójkąty prostokątne, w których szczebel jest krótszą przyprostokątną, a jego odległość od podstawy drabiny dłuższą. Jeśli suma n kątów naprzeciw szczebli (niekoniecznie kolejnych), czyli przy wierzchołku O (po jednym z każdego z n trójkątów; n>1) równa jest 45 stopni, to wszystkie szczeble-przyprostokątne w tych n trójkątach są do usunięcia.
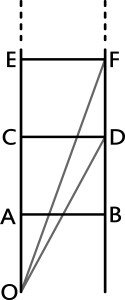
Zakładamy, że długości szczebli, odległości między szczeblami oraz odległość od podstawy drabiny do pierwszego szczebla – są takie same. Wówczas początek eliminacji szczebli jest prosty: suma kątów COD i EOF równa jest 45 stopni (dlaczego?), więc szczeble CD i EF usuwamy. Dalsza eliminacja polega na wyszukiwaniu n-elementowych (n>2) podzbiorów szczebli, dla których suma odpowiednich kątów daje 45 stopni.
Które następne szczeble kwalifikują się do usunięcia? Kto usunie najwięcej szczebli?

Komentarze
Wydaje mi się, że ci euro parlamentarzyści głównie wywodzą się z Polski. Świadczy o tym sposób realizacji idei. Idea jest porywająca, dająca wspaniałą perspektywę zdobycia kosmosu przez każdego z nas. Pod hasłem „kosmos dla każdego” można zyskać wielu zwolenników w czasie wyborczym, bo hasło „każdy może zajść dowolnie wysoko” jest bardzo nośne. Takie nośne idee, by były bezpieczne w realizacji, nasi wybrańcy zwykle obwarowywują specjalnymi warunkami. Oczywiście te warunki wprowadzane są tylko dla dobra wyborców i w trosce o nich.
Dlatego z tej wspaniałej drabiny, dającej tak niespotykane możliwości, po parlamentarnych poprawkach został tylko pierwszy szczebel.
I to jest wspaniałe rozwiązanie problemu!
Każdy może próbować, każdy ma szansę, a to że donikąd nie dojdzie dowie się sam, kiedy spróbuje. I tak to się kręci w tej polityce.
Matematyczny dowód później.
Mój pomysł na uporanie się z problemem polega na zastąpieniu kąta wyznaczonego przez n-ty szczebel drabiny dwoma kątami, wyznaczonymi przez szczeble i oraz j, które w sumie dają kat wyjściowy. Związek pomiędzy n,i,j jest następujący:
(i-n)*(j-n)=n^2+1.
Wychodząc z zamieszczonego rysunku wyjściowy zbiór numerów szczebli {2,3} według powyższego algorytmu zastępuję zbiorem {2,4,13}. Powtarzałem działania dopóki 10 najniższych szczebli drabiny pozostało nienaruszonych, natomiast zostały usunięte szczeble położone wyżej, w ilości 20, o następujących numerach:
{11, 12, 13, 14, 15, 17, 18, 21, 31, 32, 43, 50, 57, 72, 73, 81, 91, 98, 111, 183}. Oczywiście operację można powtarzać bardzo długo, lecz po wymyśleniu algorytmu było to działanie jałowe.
Serdecznie pozdrawiam, martwiłem się o Pana wobec tak długiej przerwy w prowadzeniu bloga.
Czy szczeble raz usunięte nie biorą już udziału? Jeśli usuniemy szczeble 2 i 3, a okazałoby się, że np. 3 z 4 i 6 też by pasowało, to nie można na tej podstawie usunąć 4 i 6? Teoretycznie wydaje się możliwe, że jeden szczebel pasuje w różnych zestawach, np. (zmyślam) 4, 6 i 8 oraz 4, 5 i 10. Czy wtedy należałoby usunąć 4, 6 i 8, bo zestaw się szybciej kończy, 8<10, czy 4, 5 i 10, bo następny kolega jest bliżej, 5<6? A może oba, no ale wtedy trzeba by było też dalej sprawdzać 2 i 3? Chodzi właśnie o ten algorytm usuwania szczebli 🙂
Nie można dwa razy usunąć tego samego szczebla. Ale można zacząć od usunięcia szczebli [a,b] lub [a,c,d] lub [a,e,f,g] – gdyby każdy z tych wariantów wyczerpywał rozwiązania, to ten ostatni 4-elementowy byłby oczywiście najlepszy. Można by go jednak przebić, gdyby udało się usunąć szczeble [a,b] i [c,h,j].
Istotna jest tylko łączna liczba usuniętych szczebli (zasięg usunięć nie ma znaczenia).
mp
czy długość szczebla jest równa odległości między dwoma kolejnymi szczeblami? czy może nie ma to znaczenia?
Jest równa (to istotne).
mp
Nie ma innych rozwiązań niż (2,3)
udało się usunąć trzy szczebelki
dwa różne rozwiązania to:
2, 4, 13
oraz
2, 5, 8
Faktycznie, rozwiązań jest nieskończenie wiele, np.
2 3
2 4 13
2 4 14 183
2 4 14 184 33673
2 4 14 184 33674 1133904603
Te rozwiazania generuje ciąg c_{n+1} = c_n^2 – c_n + 2; c_1 = 1. Wybieramy podciąg c_2,…,c_k i ostatni element zmniejszamy o 1, przy k = 3,…,\infty
Prawdopodobnie istnieją też inne rozwiązania, tylko muszę poprawić program…
2 3
2 4 13
2 4 14 183
2 4 14 184 33673
2 4 14 184 33674 1133904603
3 4 5 47
3 4 5 48 2257
3 4 5 48 2258 5096307
4 5 6 7 28 3583
4 5 6 7 28 3584 12841473
5 6 7 8 9 22 1918
5 6 7 8 9 22 1919 3680643
6 7 8 9 10 11 19 2334 6047163
Wysoko po tej drabinie nie wejdziemy…
Co powinno się dać udowodnić matematycznie.
Następne: (4,5,7,8,13) (6,9,10,12,17,18,21,23,30,31,32,73,91),
Udzieliła mi się podejrzliwość Grace i zacząłem się zastanawiać czy aby projekt drabina to nie jest po prostu jakiś kosmiczny przekręt w najlepszym unijnym stylu.
Postawiłem więc sobie pytanie jak uzasadnić, że możemy usunąć dowolnie wskazany szczebel o numerze n.
Wystarczyłoby pokazać, że dla dowolnego n potrafimy skonstruować wzór typu:
arctg(1)=coś+arctg(1/n).
No i eureka, takim wzorem jest np.:
Arctg(1)=arctg(1/2)+arctg(1/(1+3+3^2))+arctg(1/(1+4+4^2))+…+
arctg(1/(1+(n-1)+(n-1)^2))+arctg(1/n)
przykład dla n=5
arctg(1)=arctg(1/2)+ arctg(1/(1+3+3^2))+arctg(1/(1+4+4^2))+arctg(1/5)
arctg(1)=arctg(1/2)+ arctg(1/13)+arctg(1/(21))+arctg(1/5)
Dowód:
przyjmijmy, że x, a, b to numery szczebli – każdy następny jest większy od poprzedniego.
Mamy więc najprostszy przypadek, gdzie suma ma dwa składniki, czyli n=2 i wtedy równanie opisujące warunek z zadania jest takie:
Arctg(1/x)=arctg)1/a)+arctg(1/b)
Ponieważ mnożenie liczb zespolonych to dodawanie odpowiednich kątów, więc w języku liczb zespolonych możemy to zapisać równaniem
k(x+i)=)a+i)*(b+i), gdzie k>0
Po wyrugowaniu k otrzymujemy równanie diofantyczne
X^2+1=(a-x)*(b-x)
Teraz pomysł polega na zastąpieniu szczebla x szczeblem x+1 oraz jakimś dalszym szczeblem. No to liczymy ten dalszy szczebel. Podstawiamy a=x+1 i wyliczamy b=x^2+x+1.
Wychodząc z równania przykładowego zastępujemy szczebel 3 szczeblem 4 i szczeblem (3^2+3+1),następnie szczebel 4 szczeblem 5 i szczeblem (4^2+4+1) i tak dalej … dochodzimy do pięknego wzoru zawierającego dowolnie wysoki szczebel.
Wniosek: w drabinie zostaje tylko pierwszy szczebel, a więc minimum, żeby można było mówić o drabinie.
A swoją drogą przydałaby się jakaś komisja śledcza dla zbadania przetargu na wybór firmy utylizującej szczeble. Nie zdziwiłbym się gdyby okazało się, że głównymi jej akcjonariuszami są unijni komisarze. Przecież trzeba jakoś dorobić do pensji.
Rozwiązanie Jędrka na liczbach zespolonych:
(a+i)(b+i) = k(n+i), gdzie i jest jednostką urojoną
ab-1 = kn, a+b = k
ab-1 = (a+b)n
(a-n)(b-n) = n^2+1
a i b bierzemy z faktoryzacji n^2+1 , np.
a = n+1, b = n^2+n+1
====
można udowodnić, że dla dowolnego zbioru A szczebelków o sumarycznym kącie < 45 można wybrać zbiór B szczebelków takich, że suma kątów w A + suma kątów w B = 45; nie jestem tylko pewien, jak wykazać, że A i B mogą być rozłączne. Prawdopodobnie do eliminacji powtórzeń można posłużyć się konstrukcją Jędrka. Dlatego rację ma Grace: z drabiny zostanie tylko pierwszy szczebelek.
Na początku, chcę przeprosić wszystkich zaciekawionych moim pierwszym wpisem, że tak długo nie odzywałam się, ale czas tak szybko biegnie.
Wracając do rozwiązania zadania, najpierw wersja dla pesymistów, czyli rozwiązanie przybliżone:
(1) 1/n=tg(qn),
(2) 1/(x+1)=tg(q(n+1)).
Dla małych wartości kąta qn mamy:
(3) qn=tg(qn).
Im qn jest mniejsze tym zależność (3) jest prawdziwsza.
Z warunków zadania kąty o wierzchołku O do poszczególnych stopni drabiny mają tgqn=1/n, czyli tg(qn)=qn=1/n.
Dla małych wartości kątów suma tangensów równa się sumie kątów, czyli sumie ułamków w postaci 1/n.
Do rozwiązania zadania wystarczy dla każdego kąta 1/n znaleźć takie wartości kątów, aby suma była 1 bo tg(45)=1.
Liczba 1 jest liczbą wymierną. Ułamki 1/n są również liczbami wymiernym. Każdą liczbę wymierną można przedstawić jako sumę skończonej liczby ułamków w postaci 1/n.
Na przykład: 1= 1/2+1/3+1/6.
To znaczy, że dla wszystkich liczb wymiernych w postaci 1/n można znaleźć sumę skończonych liczb wymiernych też w postaci 1/n, aby w sumie dawały 1.
A to oznacza, że w drabinie zostanie tylko pierwszy szczebel!
A teraz rozwiązanie dla optymistów, czyli rozwiązanie dokładne.
W ogólnym przypadku kąt qn=arctg(1/n) lub 1/n=tg(qn).
Funkcja tangens i odpowiednio arcustangens są to funkcje nieliniowe i przestępne. To znaczy związek między qn i tg(qn) jest granicą nieskończonego szeregu, czyli szeregu mającego nieskończoną liczbę składników. Wartość tej funkcji dla rzeczywistych argumentów jest liczbą niewymierną przestępną.
Żadna liczba wymierna nie da się przestawić w postaci sumy skończonej ilości liczb przestępnych, więc żadna skończona ilość kątów o wierzchołku w punkcie O i tangensach w postaci 1/n nie może dawać wymiernej wartości kąta 45, albo Pi/4 radianów.
A to oznacza, że drabina zachowuje wszystkie szczeble!
Pocieszający wniosek z tego zadania jest taki, że pesymistom się tylko wydaje, że mają rację.