Kwadratoid
Rozcinamy kwadrat wzdłuż przekątnej. Jedną część obracamy o kąt mniejszy niż 90 stopni i przesuwamy tak, aby boki obu części się przecięły.
Między częściami powstała figura, której dwa przeciwległe kąty – i tylko te dwa – są proste. Nazwiemy ją kwadratoidem.
Znam przynajmniej dwa ciekawe zadania związane z taką figurą – jedno całkiem poważne i drugie nie tak całkiem. Pierwsze pasuje raczej do innego bloga, więc proponuję to drugie.
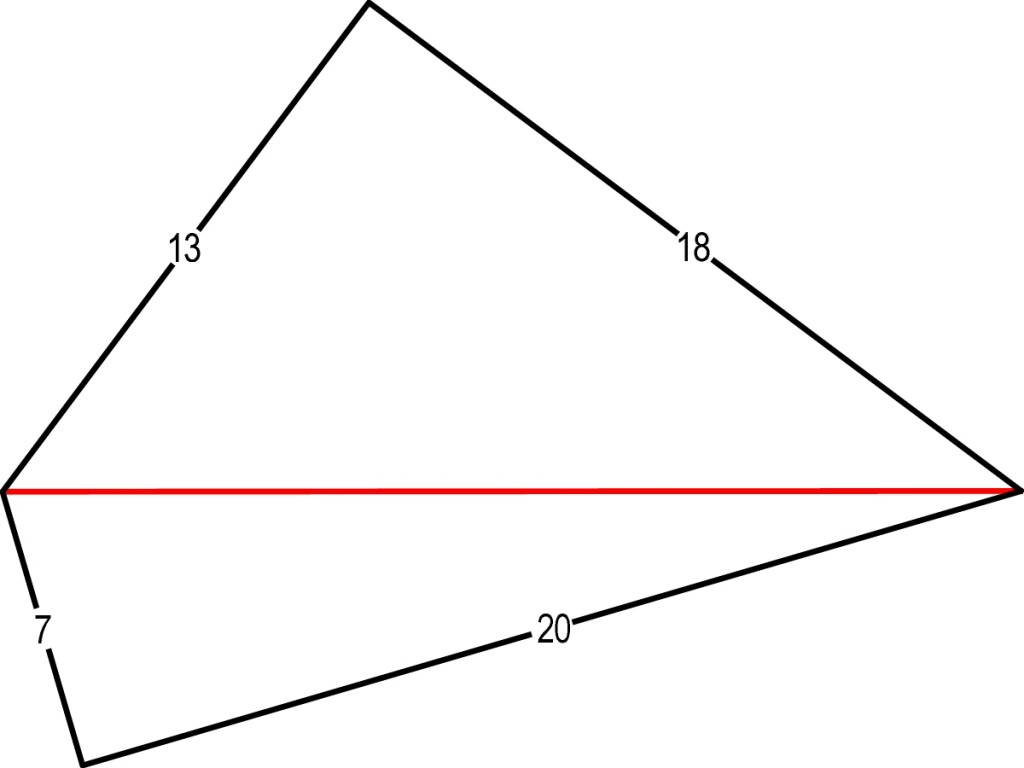
Na rysunku podane są długości boków kwadratoidu. Jaka jest długość czerwonej przekątnej?
Aby rozwiązać to zadanie nie wystarczy mieć piątkę z twierdzenia Pitagorasa.


Komentarze
Zadanie wydaje się być na poziomie trudności szkoły średniej, wieczorkiem siądę do rozwiązania 🙂
Panie Marku prowadzi Pan jeszcze innego bloga z łamigłówkami?
Nie, myślałem ogólnie o innym blogu mocniej matematycznym.
mp
tak na szybko: przekątna ma długość sqrt(493) lub sqrt(449).. dziwne, na pewno wszystko jest dobrze pomierzone? bo trochę to wbrew matematyce tak na pierwszy rzut oka… /sqrt=pierwiastek kwadratowy/
Błędu w pomiarach nie ma, ale oczywiście „coś” w tym jest.
mp
Przekątna ma długość 21, zapisaną (podobnie jak pozostałe wymiary) w układzie duodecymalnym
Długości boków podane są w systemie dwunastkowym stąd długość przekątnej to 21 (również w dwunastkowym), a w naszym przyzwoitym dziesiętnym będzie to 25 🙂
Witam panie Marku.
21 (25 w systemie 10)
i pozdrawiam tropikalnie PM.
Figura ma błąd – nie może istnieć figura z takimi założeniami (długości boków i kąty)
Jeśli założymy że trójkąt z bokami 7 i 20 jest prostokątny, to żeby pozostałe boki miały założoną długość (13 i 18) kąt pomiędzy nimi musiałby wynosić ok. 84,61?
A jakie byłoby pierwsze (poważne) zadanie?
Ale to też jest poważne, tzn. błędu nie ma, jest tylko coś, na co trzeba wpaść (i tylko dlatego jest odrobinę „niepoważne”).
mp
—
Spróbuję nie zapomnieć i za parę dni tu zaglądnąć.
Byłbym w stanie narysować taki ‚kwadratoid’
na kuli, ale chyba byłoby to za łatwe rozwiązanie?
20:57, . 27.07.2013
—
PS;
Oczywiście ważne byłoby
obliczenie promienia kuli.
Nieee! To za skomplikowane!
21:03
Przy czerwonej linii powinna zostać podana długość: 21.
Jeśli nie chcemy szukać odpowiedniej podstawy systemu liczbowego metodą prób i błędów to możemy rozwiązać równanie kwadratowe:
(1*p+3)^2+(1*p+8)^2=7^2+(2*p+0)^2
wychodzi z tego p=12 i p=-1
Ciekawe jak mógłby wyglądać system o podstawie -1, jakie miałby mieć cyfry ? Zagadnienie wygląda mało zachęcająco ale kiedyś też nie wierzono, że pierwiastek z -1 istnieje 😉
Nie ma takiej figury,jesli rysunek jest dwuwymiarowy.Moze istniec tylko,jesli:
-figura jest narysowana na powierzchni trojwymiarowego obiektu (na przyklad kuli,jak sugeruje eggerger),badz:
-jednostki miary pochodza z roznych skal.
Panie Marku, ktory z tych warunkow jest spelniony?
Przy pierwszym warunku zadanie byłoby zdecydowanie za trudne, a drugi byłby nie fair. Jest jeszcze trzecia możliwość.
mp
Eureka! Zapis w ukladzie dwunastkowym. Czyli dlugosc przekatnej 21 (25 po naszemu).
a
Czy podane długości boków są wyrażone liczbami w systemie dziesiątkowym/dziesiętnym?
To jest bardzo dobre pytanie 🙂
mp
Długości wyrażone są nie w systemie dziesiętnym, ale dwunastkowym! Po przeliczeniu:
18 -> 20
13 -> 15
20 -> 24
7 -> 7
20 * 20 + 15 * 15 = 400 + 225 = 625
24 * 24 + 7 * 7 = 576 + 49 = 625
przyznam uczciwie, nie przeliczalem ale tak na szybko to wyglada mi to na czworoscian a nie na 2 trojkaty zlaczone podstawami
Czy jest to rzut prostopadły kwadratoidu, który został obrócony względem boku, który zachował długość 20?
Pudło
mp
Czy czerwona linia jest linią zagięcia?
Nie
mp
Czerwona linia to plaszczyzna widziana z boku? Wtedy jednak czarne linie nie byłyby w jednej płaszczyźnie.
Długości boków figury podane są w dwunastkowym systemie liczbowym. Długość przekątnej (wyrażona w tym samym systemie) wynosi 21.
@bk:
W pokoju mam 29,6° C, na zewnątrz jest JESZCZE 36,4°,
ale czworościanu- z ‚tylną’, niewidoczną, krawędzią
13#18— 7#20 też nie da się „zobaczyć”.
Bo „podstawę” i „przód” czworościanu
ZE WSPÓLNA KRAWĘDZIĄ można narysować dwuwymiarowo.
A o długość tej „krawędzi” chodzi w zagadce.
I o Pitagorasie mamy zapomnieć- tylko myśleć.
Boki przecinają się ale nie na tej samej płaszczyźnie.
Katy w obu trojkatach nie sa proste.
—
Gdyby wymiary boków były zapisane
w systemie dwunastkowym, to długość
przekątnej ‚kwadratoidu’ wynosilaby ….
policzcie sobie sami.
Upal zelżał.
22:32
—
No dobra!
21.
W dwunastkowym.
Idę spać! Jutro do pracy!
22:41
Witam raz jeszcze. Jak się uważnie przeczyta treść to jasne jest, że figura musi być płaska. Sktąd już krok do rozwiązania, a promień okręgu opisanego i promień najmniejszej kuli opisanej na tym kwadratoidzie to oczywiście połowa czerwonej przekątnej 🙂
Pozdrawiam PM.
Długości boków podane są w systemie 12. Odpowiadające im liczby w systemie 10 to 7-7; 13 – 15; 18 – 20; 20 – 24. Wówczas stosując (a jednak) twierdzenie Pitagorasa otrzymujemy 24^2+7^2=625 oraz 20^2+15^2=625 i długość przekątnej sqrt(625)=25.
Rozgorzała dyskusja, więc i ja dorzucę mój pomysł, którego na razie nie potrafię zrealizować do końca….
Moim zdaniem kwadratoid został wpisany w okrąg, następnie został obrócony wokół średnicy, czyli czerwonej przekątnej. Wymiary które widzimy są rzutem na płaszczyznę. Tylko na razie nie mam pomysłu (może z powodu tych temperatur 😉 jak to policzyć, żeby nabrać pewności.
Tylko właśnie wydawało mi się, że koniec końców dojdziemy do Pitagorasa… a Pan, Panie Marku pisze, że mamy zapomnieć o Pitagorasie, więc może się pomyliłem (co jest wysoce prawdopodobne 😉 )
Nie pisałem, żeby zapomnieć o Pitagorasie, a tylko, że Pitagoras nie wystarczy.
mp
W poprzednim komentarzu opisałem problem niejasno; poniżej poprawka:
Kwadratoid został wpisany w okrąg, który został następnie obrócony wokół średnicy, która pokrywa się z czerwoną przekątną kwadratoidu. Wymiary, które są przedstawione na rysunku, są wymiarami rzutu na płaszczyznę na której leżał okrąg przed obrotem.
Coś czuję, że doświadczony krystalograf rozwiązał by to zadanie raz, dwa ;P
Nic tu po krystalografii.
mp
Szanowny Panie Marku Penszko!
To zadanie nie ma rozwiązania, a poza tym to zostało ono nieuczciwie przedstawione, jako iż figura z takimi rozmiarami nie może być utworzona na płaszczyźnie z kwadratu bez zniekształcenia jego kątów. A tymczasem wyraźnie jest widać, iż ma ona dwa kąty proste (co potwierdziłem zresztą empirycznie mierząc je kątomierzem oraz sprawdzając przy pomocy dokładnego kątownika ślusarskiego) – ten na ‚skrzyżowaniu’ boków mających na rysunku oznaczenia 18 i 13 oraz ten na ‚skrzyżowaniu’ boków mających na rysunku oznaczenia 7 i 20.
Tak więc są to trójkąty prostokątne, bo też i muszą one być prostokątne, jako iż utworzono je na płaszczyźnie z kwadratu. Wynika z tego, że wychodząc z górnego trójkąta, to czerwona linia powinna mieć długość około 22.2 cm, a wychodząc z dolnego trójkąta, to czerwona linia powinna mieć długość około 21.2 cm. Wniosek jest więc prosty ? podał Pan (mam nadzieję, że nie celowo) nieprawidłowe długości boków tych trójkątów, co zwyczajnie nie jest uczciwe. 🙁
Z kwadratoidem w istocie wszystko jest tip-top – zgodnie z definicją idealnie wpisuje się w okrąg, gdzie przekątna jest średnicą. Zatem problem jest tylko z oznaczeniami długości boków.
http://bankfotek.pl/view/1541450
Długość przekątnej to 21 🙂
Hint: podane długości są liczbami w systemie dwunastkowym
Trzeba uzależnić wartości kątów – tych, które powinny być proste, a nie są – od boków, wspólną częścią równań dla obydwu trójkątów jest oczywiście czerwona krawędź i fakt że suma kątów to 180 dla trójkątów i 360 dla czworokąta. Należy to zrobić w wersjach obróconej oraz płaskiej, w drugim przypadku każdy z boków ma nieco inną długość, ale za to oprócz zależności kątowych obowiązuje jeszcze twierdzenie Pitagorasa. Sedno sprawy m.in w tym, jak zmieniają się długości boków i kąty takiego obracanego w 3D trójkąta (tu nawet dwóch ze wspólnym bokiem i kątami prostymi w jednym z wierzchołków).
Oczywiście to wszystko przy założeniu, że jest to kwadratoid obrócony względem czerwonej krawędzi, czemu na razie Pan Marek nie zaprzeczył…
No cóż, najbliżej chyba był „tomash”?
Żeby stwierdzić, że te kąty, co miały być proste – na rysunku nie są, to wystarczy przyłożyć kartkę do ekranu.
Pozostaje pytanie – czemu? Z założeń zadania wygląda to tak, jakbyśmy mieli pełną swobodę w ostaleniu długości wszystkich boków „kwadratoidu (byle były mniejsze niż bok kwadratu podstawowego). Tu jednak nie ma 4 stopni swobody – gdy już dobierzemy 3 boki, to 4-ty jest zdeterminowany, inaczej boki się nie przetną. A „na straży” stoi właśnie Pitagoras (albo obrazowo mówiąc, ta „przekątna”). Inaczej a^2+b^2=c^2+d^2 dla dowolnych a, b, c i d. Nie ma tak dobrze.
Możnaby pewnie zrobić w ten sposób jakiś „suwak” dla obliczania pierwiastków.
Do GPSe: Nie krystalograf tylko kryptograf 🙂
jeden z trójkatów jest częściowo niewidoczny
Coś ten kwadrat na 1. rysunku mało kwadratowy.
Ja mam pomysł trochę inny: skoro rzecz nie polega na sztuczkach geometrycznych, to tajemnica kryć musi się w liczbach. One są właściwie podane bez żadnego komentarza. Dlaczegóż więc mają oznaczać takie zwykłe długości boków w używanym przez nas najczęściej systemie dziesiętnym. Sprawdziłem parę innych systemów, poczynając od 9-tkowego (mniej się nie da, ze względu na cyfrę 8) i okazało się, że już przy systemie dwunastkowym mamy pożądany wynik:
18(12) = 20(10)
13(12) = 15(10)
20(12) = 24(10)
7(12) = 7(10)
I dalej w systemie dziesiątkowym: 20^2 = 400, 15^2 = 225
24^2 = 576, 7^2 = 49.
400+225 = 576+49 = 625 (=25^2, co nie ma specjalnego znaczenia).
Mam nadzieję, że chodziło właśnie o to, pozdrawiam.
11,2 cm
o nie 22,4 cm
a w zasadzie 22 cm
A moze dlugosci bokow kwadratoidu podane sa w przyblizeniu? Jesli boki mialyby dlugosci 7,1 / 20,3 / 12,5 / 17,5 wtedy czerwona linia jest pierwiastkiem z 462,5 (okolo 21,5058)
Do Michał S.: Gra Finanse – prywatyzacja po polsku, ma zadziwiająco skąpy opis czyżby na skutek interwencji MSW ;););)
Do Spytka z Melsztyna: To tylko lenistwo właściciela strony. Podstrona z tą grą została utworzona już dawno, w międzyczasie producent zmienił pudełko gry (i usunął podtytuł „Prywatyzacja po polsku”) i nie zostało to do tej pory zaktualizowane. Ale przed chwilą to zrobiłem 🙂
21 albo 25
W sumie proste, ale przyznam się, że dopiero Michał S. mnie na trop naprowadził
—
Hmmm.
Jeśli do tej pory moje rozwiązanie
pt. „21” czeka na moderację,
to jest prawidłowe.
21:12
—
@Marta
–
Wymiary są podane dokładnie,
bez przybliżeń i są liczbami CAŁKOWITYMI.
Nawet potrzebny pierwiastek można wyliczyć
w głowie, bez kalkulatora.
Pzdr.
21:19
eggerger pisze prawdę, po prostu tak jak już Pan Marek napisał piątka z tw. Pitagorasa to za mało na to zadanie.
Fajne. Jak już się wyjdzie z etapu „to niemożliwe”.
Liczby są podane w systemie dwunastkowym odpowiedź to 21 (lub 25 w systemie dziesiętnym)
Ktoś rozwiązał to zadanie?
Tak, jutro wieczorem uwolnię komentarze z rozwiązaniem
mp
Z tym zadaniem wystarczy się przespać, tak jak ja to zrobiłem.
—
@stud.
Napisałem, że o Pitagorasie mamy zapomnieć.
Prawda- zupełnie, ale na początku.
Jak się już pomyśli, to potem warto
jego prawo znać. Hihihi.
😉
19:27
—
Panie Penszko.
Czy mógłby Pan podać jutro WYNIK- tylko,
tego ‚poważniejszego’ rozwiązania?
Ciekawi mnie średnica tej kuli
i długość przekątnej. W dziesiętnym.
PS.
Wielka szkoda, że Matka Ewolucja
nie dała mam SZEŚCIOPALCZASTEJ dłoni.
Byłoby łatwiej liczyć.
19:41
Jutro wieczorem po prostu uwolnię wszystkie komentarze z poprawnym rozwiązaniem.
mp
PS także niniejszy z „sześciopalczastą” podpowiedzią 🙂
Chciałem zauważyć, że wakacje powoli się kończą. Tu pretensje…, gdzie są pestki wakacyjne ? (o orzeszkach i twardych orzechach nie wspominając). Tu sentencja. Jeden kwatrotoid wiosny nie czyni.
Sorry. Nowe wakacje – nowa koncepcja, a właściwie jej brak, czyli – jak mówi Kimi – I’ve no idea.
mp
Bez większej nadziei: Czerwona przekątna jest średnicą okręgu opisanego. Długość średnicy jest sumą długości 2 promieni. Każdy z tych promieni można policzyć Pitagorasem. Wyjdzie wtedy sqrt(123,25) + sqrt(112,25). A promienie nie są równe, bo zadanie nie tak całkiem poważne…
A może w ramach wakacyjnej pestki czy też orzecha poprosimy Pana Marka o zaserwowanie nam tego trudniejszego KWADRATOIDU. Jeśli nie jako temat główny to chociaż boczny. Jedyne co nam grozi to tylko totalna porażka i połamanie wirtualnych zębów 😉 😉 ;). Ale przynajmniej będzie burza mózgów.
To zadanie czeka na publikację w innym miejscu, więc nie mogę go tu ujawniać – przynajmniej na razie. Przepraszam za narobienie smaku 🙂 .
mp
Jeżeli te wymiary są podane w systemie innym niż dziesiatkowym, to dobre zwyczaje wymagają, aby dodać do nich tzw. subkrypt, podający w jakim systemie są one zapisane. Inaczej, to ja mogę Panu Penszko ofiarowac ‚od ręki’ oraz gotówką milion zł (PLN 1000000), ale w systemie dwójkowym, czyli 64 zł (PLN 64) w systemie dziesiątkowym.
Panie Marku a co to za inne miejsce gdzie publikowane są zadania matematyczne? Myślę, że nie tylko ja tu jestem głodny ciekawych łamigłówek 😉
Może Pan podać link?
To nie internet, to papier, w dodatku nie polski i jeszcze nie mam 100% pewności, czy będzie opublikowane.
Przyrzekam, że wrócę do tego zadania, gdy będę mógł.
mp
Do kagana: Gdyby takie zadanie było na teście dla gimnazjalistów, to oczywiście stosowna byłaby takowa podpowiedź. Ale ta łamigłówka została zamieszczona na blogu dla koneserów łamigłówek i to łamigłówek trudnych i w pewnym stopniu przypomina publikowane tu zadania indukcyjne, polegajace na tym, że trzeba najpierw znaleźć „klucz” do zadania i dopiero wtedy je rozwiązać
Otóż to! Ja miałem wrażenie, że kagan żartuje.
mp
Do kagan: Wpadłeś na znakomity pomysł 🙂 Zgłoś go tylko do Konfederacji Pracodawców LEWIATAN. Niech rozpropagują pomysł, żeby kwota wynagrodzenia w umowie o pracę była wyrażona w systemie dwójkowym a umowa na 30 lat bez możliwości żadnych zmian. Pracownik będzie odkrywał prawdę dopiero przy kasie albo na rachunku bankowym 😉 Dzięki temu pracodawcy będą bogatsi i stworzą więcej miejsc pracy, a przecież właśnie o to chodzi. Polska ruszy z kopyta a Ty zostaniesz nowym ministrem finansów czego Ci szczerze życzę 🙂
pytanie: 30 lat w jakim systemie liczbowym 😉
Do Spytka z Melsztyna: Ale te „30 lat” też powinno być zapisane w systemie dwójkowym jako 11110 i wtedy łatwo odkryć podstęp 🙂
Kagan po prostu za bardzo się „wciągnął” w zadanie 😉
Sam przez dwa dni miałem zły humor, nie jadłem i nie spałem, ba! nawet nie pracowałem! Tylko myślałem o kwadratoidzie niepitagorejskim. Ale niestety… Moje myśli krążyły w tak bardzo odległych obszarach od rzeczywistego rozwiązania, że chyba po miesiącu myślenia bym nie wpadł na rozwiązanie 😉
Bardzo dobre zadanie 🙂 proste do narysowania w towarzystwie, spróbuję, może nikt ze znajomych ani członków rodziny się na mnie nie obrazi… 😉
mały off-top się zrobił 😉
proponuję zająć się labiryntem jeśli jeszcze ktoś nie zrobił, a jak ktoś zrobił to czekać grzecznie na kolejne zadanie
Jeśli myślimy w duchu „prywatyzacji po polsku” to oczywiście „30 lat” powinno być zapisane w systemie dziesiętnym aby „ofiara/pracownik” nie mogła się łatwo połapać. A jeśli myślimy normalnie to taka organizacja jak LEWIATAN nie miałaby prawa/sensu istnieć bo powszechny byłby AKCJONARIAT PRACOWNICZY i stosowanie jakichkolwiek sztuczek świadczyłby o rozdwojeniu jaźni pracodawcy będącego jednocześnie pracownikiem 🙂
@Michał @ Spytko & GPSE
1. Michale – to, że dana łamigłówka została zamieszczona na blogu dla koneserów łamigłówek i to łamigłówek trudnych , bynajmniej nie usprawiedliwia tego, że podana ona została nieuczciwie, co wykazuje doskonale moja propozycja przekazania Panu Penszko kwoty 1000000 złotych, tyle że zapisanych w systemie dwójkowym. Jeśli ja bym wystawił tam gdzie mieszkam czek na 1000000 dolarów, to nikt by nie przyjął tłumaczenia, że miałem na mysli zapis w systemie binarnym, a więc miałbym spore kłopoty wynikłe z rozmyślnego wystawienia czeku bez pokrycia, nie mówiąc już o tym, że straciłbym w ten sposób honor, zaufanie i twarz.
2. Spytku – z Lewiatanem nie chcę mieć nic wspólnego, z powodów, które łatwo jest się domyśleć. Po prostu nie mógłbym po tym spojrzeć na swoje odbicie w lustrze.
3. GPSE – Wystarczyło wyciąć cienkie patyczki o wymiarach jak podanych przez P. Penszko, aby się przekonać empirycznie, że taka figura istnieć nie może – po prostu wymiary podane przez P. Penszko wymagają eliminacji kątów prostych, a P. Penszko wyraźnie napisał, że nie ma mowy o zmianie kątów, a tylko mowa jest o przesuwaniu fragmentów kwadratu po płaszczyźnie, czyli bez zmiany kątów.
4. Mam więc nadzieję, że Pan Penszko przeprosi publicznie na tym blogu ofiary swego nieuczciwego podstępu oraz iż przekaże mi odszkodowanie w wysokosci 1000000 zl, tyle, że zapisanych w systemie dwójkowym.
Pozdrawiam!
Niestety, wygląda na to, że kagan pisze na ogół poważnie. Jeśli tak, proszę o uszanowanie tej powagi, bo chyba nic się na nią nie poradzi. Jeśli nie (p. 4), proszę się uśmiechnąć i spróbować powstrzymać się od dalszych komentarzy (oczywiście, jeżeli się pojawią – z zachowaniem bon tonu – będę je uwalniał).
mp
Panie Marku, ja również jestem zawsze bardzo poważny 😉 Zazwyczaj nie zaglądam do gotowych rozwiązań, jeżeli nie zdążę rozwiązać łamigłówki przed uwolnieniem komentarzy z prawidłowymi rozwiązaniami, tylko myślę tak długo, aż znajdę poprawną odpowiedź (nie zawsze da się cały dzień w pracy myśleć o łamigłówkach zamiast o pracy 😉 ). Kwadratoid sprawił, że nie wytrzymałem i zajrzałem… I był to doskonały pomysł, ponieważ lada dzień wyobraziłbym sobie przestrzeń 5,5 wymiarową, rzucił laptopem o ścianę, podarł wszystkie moje książki o matematyce. Ani na chwilę nie przyszło mi do głowy, że problem tkwi w zapisie długości boków. Już zaczynałem wątpić w moje możliwości intelektualne, gdy tymczasem rozwiązanie okazało się dosyć banalne. Przyznaję: że tym razem mnie Pan przechytrzył i to jak! Czuję się autentycznie przechytrzony (co nie znaczy oszukany 😉 ) Ale nie gniewam się. Wręcz przeciwnie. Dziękuję za udzieloną lekcję, z pewnością pomoże mi ona w przyszłości radzić sobie z jeszcze większymi podstępami 😉 gorąco zachęcam do stworzenia bardziej matematycznego bloga, będę jego wiernym fanem.
Pozdrawiam 🙂
Problem w tym, czy zadanie z kwadratoidem było „faulem”, czy nie. Starałem się, aby nie było, uprzedzając, że jest trochę „niepoważne”. Poza tym do głowy by mi nie przyszło, aby ktokolwiek próbował je rozwiązywać, korzystając z matematyki wykraczającej poza ogólniak. To nie ten blog. Zastosowałem też nie jakiś dziwaczny system liczbowy, tylko taki, z którego tu i ówdzie jeszcze korzystamy.
Rozumiem tych, którzy (jak kagan) czują się sfaulowani, ale – „wysoki sądzie” – nie czuję się winny 🙂 .
mp
Stali czytelnicy bloga zapewne wiedzą, że cenioną przez Autora cechą łamigłówki jest to, że posiada tylko jedno prawidłowe rozwiązanie, zaś istnienie większej ich liczby to swego rodzaju ułomność zagadki. Wobec tego, jeśli ktoś poczuł się rozczarowany odpowiedzią do zadania z kwadratoidem, to proponuję, by konstruktywnie odreagował wykazując, że istnieje więcej rozwiązań niż jedno. Im więcej tym lepiej. Wszak nie jest nigdzie powiedziane, że wszystkie długości boków kwadratoidu są wyrażone w tym samym systemie liczbowym. 😉
No, chyba, że każde takie rozwiązanie to 25 (w systemie dziesiętnym). Wtedy Autorowi należą się szczególne gratulacje.
Dowiedzenie, że taki kwadratoid ‚za który należą się szczególne gratulacje’ istnieje bądź nie, niech będzie zadaniem dla ambitnych. 😉
Przeprowadzenie dowodu na jednoznaczność rozwiązania byłoby chyba dość trudne, szczerze mówiąc nie wiem nawet od czego zacząć. Najpierw jednak sprawdziłem wszystkie systemy liczbowe o podstawie od 9 do 5000 i rozwiązanie jest tylko jedno. Dla systemów liczbowych o większej podstawie trzebaby napisać jakiś programik, bo excel nie ogarnia takich dużych liczb.
Stud, chodzi mi o rozwiązania typu:
13(a) ^ 2 + 18(b) ^ 2 = 7(c) ^ 2 + 20(d) ^ 2
Założenie a=b=c=d nie musi być spełnione. Np. dla a=4, b=16, c=8, d=12 długość czerwonego odcinka to też 25 (tak jak dla a=b=c=d=12), ale dla a=4, b=10, c=8, d=9 długość czerwonego odcinka to już ok. 19,31, a dla a=4, b=14, c=8, d=11 to ok. 23,09. Zatem zadanie nie ma jednoznacznej odpowiedzi. Takich zestawów systemów a, b, c, d jest więcej. (By powyższe zadanie miało jedno rozwiązanie to być może wystarczyłoby dodać, że czerwona przekątna jest wyrażona liczbą całkowitą i, dla pewności, mniejszą od np. 30.)
Z moich analiz również wynika, że dla a=b=c=d tylko 12 stanowi rozwiązanie.
W zadaniu ‚dla ambitnych’ zaś rzecz w tym, by znaleźć kwadratoid
A(a) ^ 2 + B(b) ^ 2 = C(c) ^ 2 + D(d) ^ 2
którego długości boków zostaną wyrażone liczbami z takimi cyframi, aby rozwiązanie zawsze było jednoznaczne, nawet jeśli powyższy warunek zostałby spełniony dla różnych zestawów a, b, c, d. Zatem, aby łamigłówka zachowała swoje pozostałe cechy i rozwiązanie było jednoznaczne, należy znaleźć takie A, B, C i D, aby:
1) nie istniało rozwiązanie dla a=b=c=d=10,
2) A, B, C, D składały się wyłącznie z cyfr z przedziału 0-9,
3) długość czerwonej przekątnej wynosiła tą samą wartość dla każdego zestawu a, b, c, d spełniającego warunki zadania,
4) (warunek dodatkowy) wśród zestawów a, b, c, d spełniających warunki zadania, istniał minimum jeden gdzie a=b=c=d.
Być może konieczne okazałyby się i inne warunki, by kwadratoid wyglądał jak najmniej ‚podejrzanie’. Np. by:
5) A, B, C, D były najwyżej trzycyfrowe,
6) ta sama cyfra niech wystąpi najwyżej trzykrotnie.