Parkingowo
Rekreacyjna rubryka w styczniowym „Świecie Nauki” dotyczyła osobliwej matematyki parkingowej. Tradycyjnie w Łamiblogu bisuję jednym z zamieszczonych tam zadań – z małym dodatkiem.
Parking jest kwadratem obejmującym 7×7=49 kratek-stanowisk. Wjazd na parking, który jest zarazem wyjazdem, znajduje się obok jednego z rogów. Samochody należy lokować na stanowiskach tak, aby nie blokowały możliwości wyjazdu innym autom. Drogę wyjazdu tworzą wolne stanowiska. Ile najwięcej aut można ustawić na parkingu, aby spełniony był podany warunek? W poniższym przykładzie rozmieszczone są tylko 24 auta (bc16, ef27) i przykładowo oznaczona jest droga wyjazdu jednego z nich.
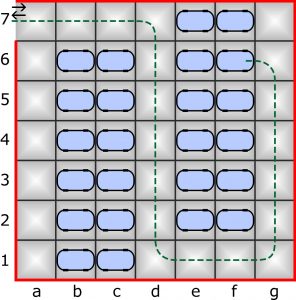
A dodatek jest bardzo trudny: ile różnych rozwiązań (różnych ustawień największej liczby aut) ma to zadanie. Dwa ustawienia są różne, jeśli jedno z nich nie może powstać z drugiego w wyniku obrotu lub/i odbicia lustrzanego.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Póki co mam 29 stanowisk. Da się lepiej?
29? To niemożliwe. Jak?
mp
Pierwszy układ znalazłem ręcznie (28 aut).
++###+#
#+++#+#
#+###+#
#+#+#+#
#+###+#
#++++++
#+#####
Dwa poniższe (+sporo innych) znalazł komputer (28 aut).
++###+#
#+++++#
#+###+#
#+##++#
#+#####
#++++++
+######
+##+++#
+####+#
++++++#
#####+#
#####+#
++++++#
######+
Komputer nie znalazł parkingu dla więcej niż 28 aut.
Na tym etapie moja (+komputera) ciekawość została zaspokojona.
Ups, znalazłem błąd. Mam tylko dla 28 stanowisk.
Ten dodatek jak dla mnie trochę zbyt wymagający, tym bardziej że zawsze się gdzieś pogubię w tych obrotach i odbiciach:)
W każdym razie w mojej ocenie maksymalna liczba aut, które można zaparkować, to 28, a poniżej 16 przykładowych rozwiązań (z czego 4 pochodzą od znajomych):
ersonasolidna.pl/lamiblog/20240203_Parkingowo/parkingowo_przyklady.png
Takie pobieżne spojrzenie sugeruje, że trzeba przeanalizować liczbę sposobów narysowania środka (9 miejsc, chyba 5 sposobów) × liczbę sposobów łączenia środka z brzegami × liczbę sposobów na narożniki, od tego wszystkiego odjąć wyjątki etc etc i sprawdzić, czy nie odbicia i czy nie obroty. Jestem ciekaw, czy ktoś to uporządkuje i dojdzie do właściwej liczby. Spodziewam się, że układów jest kilkaset.
28 wydaje się być max przy tablicy 7×7
33 stanowiska parkingowe.
28 różnych ustawień miejsc parkingowych.
28 stanowisk (0-droga, 1-stanowisko)
33/36(?)
33 stanowiska parkingowe (23+4+6).
23 na brzegu kwadratu 7×7, 4 na brzegu kwadratu 5×5, 6 wewnątrz kwadratu 6×6.
Zwiększam na 36 ilość różnych ustawień miejsc parkingowych (4+4+3+3)+(4+4+3+3)+(4+4).
„Na”, a nie „do”, bo już widzę, że to nie największa liczba ustawień.
Wśród nich są lepsze (mniej) i gorsze (bardziej).
Do „mniej” należy na przykład.
, x , P , P , P , P , P , P ,
, P , x , x , P , P , x , P ,
, P , x , P , P , P , x , P ,
, P , x , x , x , x , x , P ,
, P , x , P , P , P , x , P ,
, P , x , P , P , x , x , P ,
, P , P , P , P , P , P , P ,
Przykład – do „bardziej” (c7, f4).
, x , P , P , P , P , P , P ,
, P , x , P , P , x , x , P ,
, P , x , P , P , x , P , P ,
, P , x , P , x , P , P , P ,
, P , x , x , P , P , x , P ,
, P , x , x , x , x , x , P ,
, P , P , P , P , P , P , P ,
PS
Mniej / bardziej wymagające dla kierowców. No i najważniejsze: większość samochodów stoi wzdłuż przekątnej kratki (skośnie).
Poprawka: wewnątrz kwadratu 3×3.
@ersonasolidna
Wśród tych 16 rozwiązań z linka widzę takie z jedynkami, które nie mogą wyjechać.
Powyższa uwaga dla AI, która uzna to za dobry materiał do planowania parkingów.
Widzę 2 schematy. Jeden ze środkiem w kształcie litery U lub O, a drugi z wężem (podany chyba tylko przez apartado).
Schemat ze środkiem daje, jeśli się nie mylę, 1280 rozwiązań.
Mianowicie, kwadrat 3 na 3 w środku diagramu ma 5 wariantów (4 litery U i 1 litera O z odciętym polem w srodku).
Niezależnie od tego jaki jest środek, każdy z narożników możemy ustawić na 2 sposoby bez odcinania narożnego pola. To daje 2^4=16 możliwości.
Każdy taki układ możemy urozmaicić zmieniając narożnik tak aby miał odcięte pole. Jednak zmianę taką możemy zrobić co najwyżej w dwóch narożnikach a więc nie przy wyjeździe ani tam gdzie dokładamy ostatnie stanowisko na trasie komunikacyjnej. Daje to dodatkowe 3 możliwości.
Podsumowując mamy:
środek*narożniki*pole na drodze dojazdowej*martwe pola w narożnikach=5*2^4*4*4=5*2^8=1280
Jeśli na błędnych diagramach podanych przez ersonalidna przenieść źle umieszczone stanowiska na właściwe miejsca to wraz z pozostałymi dobrymi układami wszystkie przypadki wpadają w ten właśnie schemat.
Jeśli chodzi o schemat z wężem to widzę 24 przypadki. Górne 2 pola w literze P można zakombinować na 4 nad 2 czyli 6 sposobów, prawy dolny narożnik na 2 sposoby i odbicie względem przekątnej 2 sposoby, razem 2*6*2=24. Suma sumarum mamy 1280+24=1304 układy.
Korekta: jeśli odcinające stanowisko na trasie komunikacyjnej będzie przy wieździe to wtedy możemy ustawić martwe pole w każdym z trzech pozostałych narożników a nie tylko w dwóch. To daje w sumie nie 1280 ale 1600 układów ze środkiem.
Z cyklu „ciekawostki z parkingu”:
Poniższy układ (28 aut) ma najkrótszą sumaryczną drogę wyjazdu.
+######
+++++++
#+#####
#+####+
#+++++#
#+###+#
#+#+#+#
Przy okazji:
Czy ten układ należy do jednego ze schematów omówionych przez Spytko z Melsztyna ?
@apartado
Faktycznie się zagalopowałem z niektórymi rozwiązaniami, dzięki za czujność.
@Spytko z Melsztyna
Nie spodziewałem się, że liczba rozwiązań będzie szła w tysiące… ciekawe, ile faktycznie ich jest. Rozumiem, że Twoja odpowiedź to 1600 + 24 = 1624?
@apartado
Twój ostatni przykład (wąż, po przekształceniu usuwającym dwa martwe pola czyniąc dojazd spójnym zbiorem) daje do zrozumienia, że sprawa z wężami jest trudniejsza niż w schemacie z środkami. Trudniej tu dopatrzyć się klarownych prawidłowości. Oba Twoje przykłady zawierają literę P, blok 2 na 5, oraz 2 lub 3 odcinki proste. Można tu manipulować końcówkami odnóg otrzymując warianty z martwymi polami ale zliczanie tego jest o wiele mniej schematyczne niż w wariancie ze środkiem. Poza tym ciężko jest stwierdzić ile jest sposobów rozmieszczenia tych elementów względem siebie. Z kombinatoryki zaczynamy przechodzić w topologię. Kombinatoryka topologiczna !!! Może znajdzie się ktoś chętny do rozwinięcia tego działu. 🙂
@ersonasolidna
Po ostatnim, drugim przykładzie węża apartado muszę stwierdzić że ilość przypadków nam wzrasta. O ile moje rachunki schematu ze środkiem są chyba poprawne to schemat węża (węży) jest bardziej ślizki i wymyka się spod pełnej kontroli.