Sześć setek
W roku 2006 na 15. Mistrzostwach Świata w Rozwiązywaniu Łamigłówek, zorganizowanych w bułgarskim kurorcie Borowec, debiutowało małe, urokliwe zadanko. Oparte na prostym, ale oryginalnym pomyśle (autor Władimir Portugałow z Białorusi) uznane zostało przez wytrawnych główkołamaczy za swego rodzaju perełkę. Wydaje się trywialne do ułożenia, ale to pozory, bowiem należy zadbać o to, aby miało jedno rozwiązanie i nie było drogą przez mękę, czyli umożliwiało skorzystanie w znacznym stopniu ze ścieżki logicznej (wykluczyć całkowicie prób i błędów zwykle nie sposób).
Na starcie jest kwadrat 3×3 z cyfrą w każdym polu. Większość cyfr albo wszystkie należy uzupełnić sąsiadką, dopisując obok niej (przed lub za) odpowiednią cyfrę. Po dopisaniu w kratce pojawia się liczba dwucyfrowa. Cały ten zabieg należy przeprowadzić tak, aby suma trzech liczb w każdym z trzech wierszy i w każdej z trzech kolumn diagramu była równa 100.
Przykład
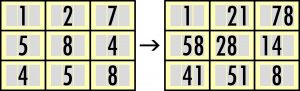
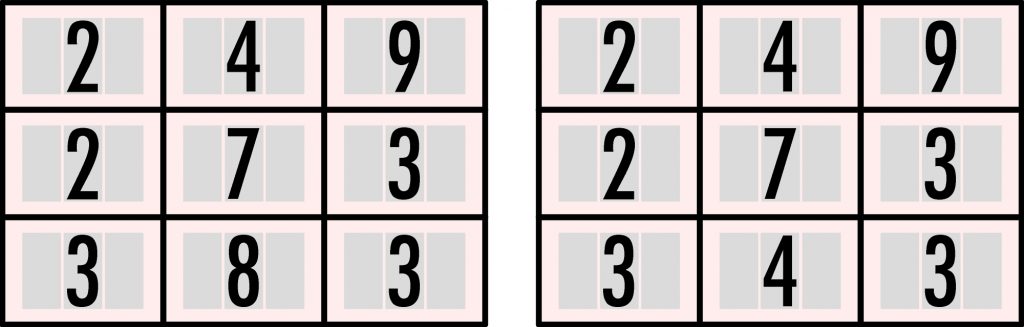
Łamigłówka bywa zwodnicza. Łatwo coś przeoczyć, a nawet dojść do wniosku, że nie ma rozwiązania. Takie podejrzenie padło początkowo na poniższą z lewej strony. Sąsiednia z prawej jest jej „bliźniaczką” – różni się tylko jedną cyfrą startową i wydaje się znacznie łatwiejsza, jeśli… wpadnie się na właściwy trop.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Pierwsze zadanie
26 45 29
21 47 32
53 08 39
Bliźniaczka ma dużo rozwiązań. Jedno rozwiązanie powstanie jeżeli 8 zamienimy nie na 4 a na 5.
Przykładowe rozwiązania bliźniaczki
12 49 39
52 17 31
36 34 30
22 49 29
25 37 38
53 14 33
32 49 19
25 37 38
43 14 43
Z zamianą na piątkę
23 48 29
24 37 39
53 15 32
W oryginalnym zadaniu liczba w lewym górnym rogu może się zmieniać od 1 do 4
i za każdym razem jest jedno rozwiązanie.
16_45_39——36_45_19——46_45_09
52_17_31——25_37_38——20_27_53
32_38_39——39_18_43——34_28_38
Naprawdę oryginalne i ciekawe zadanie!
Pierwszy kwadrat:
26, 45, 29
21, 47, 32
53, 8, 39
Drugi kwadrat (faktycznie łatwiejszy):
2, 4, 94
25, 72, 3
73, 24, 3
Na początek spróbowałem głową (chodziło mi po niej coś w rodzaju poniższego v1).
Potem użyłem sztucznej inteligencji.
zadanie 1
26+45+29=100
21+47+32=100
53+8+39=100
zadanie 2
v1
2+4+94=100
25+72+3=100
73+24+3=100
v2
22+49+29=100
25+37+38=100
53+14+33=100
v3
2+49+49=100
25+37+38=100
73+14+13=100
v4
12+49+39=100
52+17+31=100
36+34+30=100
26+45+29=100
21+47+32=100
53+8+39=100
2+4+94=100
25+72+3=100
73+24+3=100
Dla zadania drugiego numeracja „v” idzie w górę…
Ta łatwiejsza:
I ta, hm, trudniejsza:
Pierwszy diagram:
26, 45, 29
21, 47, 32
53, 8, 39.
Drugi diagram można rozwiązać na wiele sposobów. Najłatwiejszy do znalezienia wydaje się następujący układ:
2, 4, 94
25, 72, 3
73, 24, 3.
Lewe zadanie ma tylko jedno rozwiązanie:
Natomiast, zadanie przykładowe trzyma fason bo ma tylko jedno, podane, rozwiązanie 🙂
lewy diagram ma tylko jedno rozwiązanie
prawy ma 6 rozwiązań i dla mnie był dużo trudniejszy bo metoda eliminacji nie działała:
Pierwsza:
26 | 45 | 29
21 | 47 | 32
53 | 08 | 39
Druga:
02 | 04 | 94
25 | 72 | 03
73 | 24 | 03
Muszę przyznać, że najpierw rozwiązałem to niby trudniejsze, z 8:
26 45 29
21 47 32
53 8 39
W drugim przykładzie założyłem, że mogą być cztery liczby niezmienione, i okazało się, że faktycznie:
2 4 94
25 72 3
73 24 3
Na piechotę nie znalazłem rozwiązania zagadki z lewej strony, choć czułem podskórnie, że ósemkę jako jedyną trzeba zostawić bez dopisanej cyfry:) Zagadka z prawej okazała się łatwiejsza.
Wg programu – jedyne rozwiązanie zagadki po lewej:
A rozwiązań „prawej” zagadki jest 5:
Tylko pierwszą zdążyłam zrobić:
Dobry wieczór,
Lewy diagram:
26 45 29
21 47 32
53 8 39
Prawy diagram:
12 49 39
52 17 31
36 34 30
Pozdrawiam,
Spytko oczywiście ma rację, że jest 8, a nie 5 rozwiązań prawego zadania.
Chciałem „zoptymalizować” sobie algorytm i przesadziłem…
Skrypt: https://github.com/ersonasolidna/lamiblogswiatnauki/blob/8b1cb0e3f87d2f67703726817a3b3e87f76d3fbf/2023-02-11_Lamiblog_Szescsetek.py