Pętliczek
Pojawiające się w łamigłówkach diagramowych polecenie „narysuj linię…” ma często ciąg dalszy ”… łamaną zamkniętą”. Koronny przykład instrukcji z takim fragmentem gości w pokropce https://penszko.blog.polityka.pl/2008/12/15/multikropka/, która debiutowała w Japonii w roku 1989 na łamach kwartalnika „Nikoli”. W tym samym numerze czasopisma pojawiło się podobne zadanie o nazwie zrób pętlę. Zadanie nie miało pokropkowego uroku, więc jego żywot na łamach był krótki; szybko poszło w niepamięć. Przypomnieć je jednak warto, ale uprzedzam – lekko nie będzie.
Linia łamana zamknięta powinna biec białymi korytarzami. Tworzące ją odcinki składają się z jednostkowych fragmentów, czyli boków kratek, zaś każda liczba przy brzegu oznacza, ile jednostkowych fragmentów w danym korytarzu poziomym lub pionowym powinna „zaliczyć” łamana. Ponadto – w odróżnieniu od pokropki – linia może przecinać samą siebie.
Przykład
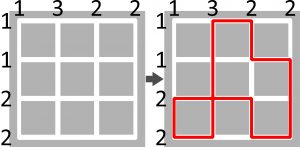
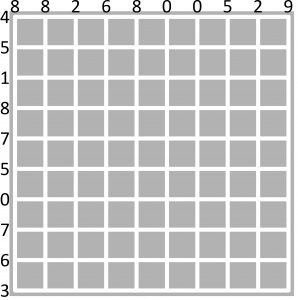
Zadanie
W rozwiązaniu wystarczy podać liczbę skrzyżowań (w przykładzie jest jedno).
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Jest 12 skrzyżowań.
Patrząc od góry diagramu w kolejnych poziomych białych korytarzach jest:
0, 2, 0, 2, 2, 2, 0, 3, 1, 0 skrzyżowań.
12
12
https://www.fotosik.pl/zdjecie/0ccb6d667c45c75d
12
12
12 skrzyżowań
Liczba skrzyżowań: 12.
Podpowiedź dla nas wszystkich:
Kiedy Nasz Miły Gospodarz pisze: „ostrzegam – to trudny orzech” (albo coś w tym przestraszającym stylu), to często zadanie wyglądające na trudne, w istocie jest łatwiejsze, niż się wydaje.
Czy tak jest tym razem ? – trudno powiedzieć.
Jak dla kogo. Trudne, łatwe – to pojęcia względne.
mp
Tuzin
Początkowo sądziłem, że zadanie będzie w pewnym momencie wymagało jakichś „zaawansowanych analiz topologicznych” lub/i znajomości „sztuczek i niuansów teorii węzłów”, a okazało się, że kolejne proste obserwacje prowadziły do kolejnego kroku – w tym sensie zadanie jest łatwe.
„Oczywiście” był taki moment, że musiałem się cofnąć o spory odcinek w czasie rozwiązywania, ale nie wynikało to z „testowania ścieżki”, tylko z tego, że po prostu popełniłem błąd.
Trudność polega chyba na tym, żeby takich błędów było jak najmniej – ja miałem jedną „wpadkę” 😉
Zaawansowana topologia, niuanse teorii węzłów – rozumiem, że to z przymrużeniem oka, bo na serio to nie w tym blogu.
mp
12
W rozwiązaniu jest 12 skrzyżowań.