Andrzej i sześciany
Kryptarytmetycy vel alfametycy zauważyli, że wyrażenie PREZYDENT ANDRZEJ składa się wprawdzie aż z 16 liter, ale jest wśród nich dokładnie 10 różnych, a ponadto PREZYDENT jest tylko trochę dłuższy niż ANDRZEJ. To sprzyjające okoliczności, aby postawić quasi-łamigłówkowe pytanie: ilu ANDRZEJów potrzeba, by powstał jeden PREZYDENT, czyli jakie jest rozwiązanie alfametyku
ANDRZEJ * x = PREZYDENT
i dla jakiego x?
To zadanie ewidentnie dla komputera, a dwa i tylko dwa rozwiązania dla x mniejszego od 100 są następujące:
4953782*28=138705896 ; 8021936*89=713952304
Czy są rozwiązania dla x>100 – tego nie wiem (choć wątpię), ale może ktoś z gości programistów rozstrzygnie ten problem.
A skoro jesteśmy przy kryptarytmach, to proponuję coś trudnego z sześcianami.
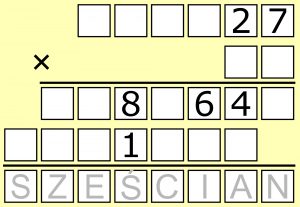
Poniższe szkieletowe mnożenie obfituje w sześciany, ale większość z nich stanowią ujawnione fragmenty liczb – mnożnej i iloczynów cząstkowych. Całym sześcianem jest natomiast iloczyn zaszyfrowany literami. Jak zwykle w kryptarytmach, różnym literom odpowiadają różne cyfry (jednakowych liter nie ma). Celem jest oczywiście rozszyfrowanie działania.
Wracając do sześcianów: sześciennych ANDRZEJów jest trzech (7-cyfrowe sześciany złożone z różnych cyfr – 2460375 (135^3), 3048625 (145^3) i 8365427 (203^3), ale sześciennego PREZYDENTa (9 cyfr, w tym tylko dwie jednakowe, odpowiadające literom E) – brak. I na tym zakończę, bo niebezpiecznie zbliżyłem się do numerologii.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
264627 * 99 = 2381643 + 10 * 2381643 = 26198073
264627 x 99
SZEŚCIAN = 26198073
264627×99=26198073=297^3
264627*99
—-
€∀∀∈∈∑∑⋂⋂!
Panie Marku, w poprzednim wpisie Skąd błąd? potęgował Pan używając zapisu x<sup>2</sup>, co na ekranie dało: x² (tu powinno być x i 2 w indeksie górnym). Skopiowałem to w moim wpisie, ale efekt był banalny: x2, czyli komentujący nie mogą indeksować. Oprócz czcionki o stałej szerokości przydałoby się dorzucić możliwość potęgowania. Wiem, że marudzę, ale jest gorąco. No i może coś wytarguję…
Pierwiastkować chyba już umiem (próba): ∀x∈R ∃y∈C: √x=y
W powyższym wpisie użyłem matematycznych symboli HTML. Przed kliknięciem w „Opublikuj” nie wiem, co pojawi się na ekranie, więc może być nieczytelny bałagan.
Przepraszam, ale czcionki o stałej szerokości raczej nie wytarguję u administratora, a potęgowanie indeksem górnym – jak wynika z Pańskiego wpisu – chyba jest możliwe.
mp
264627*99=2381643+23816430=26198073=297^3
Tak nie bardzo pojmuję, na czym polega trudność tego zadania. Wystarczyło mi 15 minut, parę założeń i proste mnożenie/dzielenie w Excelu.
Po pierwsze, żeby przedostatnia cyfra w III rzędzie była 4, to druga cyfra w II rzędzie może być tylko jedna: 9. Zatem końcówka III rzędu to 643, a SZEŚCIAN będzie się kończył na 3. Żeby ten ostatni warunek był spełniony, podstawa sześcianu musi się kończyć na 7, a takich podstaw dających 8-cyfrowy sześcian jest zaledwie 25 (od 217 do 457, co 10, bo cyfra jedności musi być 7).
Po drugie, czwarta cyfra w słowie SZEŚCIAN może być tylko cyfrą 9 lub 0, zatem z 25 zostają tylko 3 możliwości, a tylko jedna z nich spełnia wymóg różnych liter (cyfr) i jest to 26198073 (sześcian 297).
Dzieląc ten sześcian przez liczbę dwucyfrową zakończoną na 9 (II rząd) otrzymujemy tylko jeden wynik całkowity zawierający – notabene – jeszcze jeden sześcian.
Zatem:
264627 x 99 = 26198073 ( _2381643 + 2381643_ )
Pozdrawiam,
Przemek Ketner