Łaciński kawałek
Kwadrat łaciński jest podstawą wielu zadań diagramowych; powiedziałbym nawet, że większości szerzej znanych – z sudoku w roli głównej. Ale podstawą może być także kawałek kwadratu łacińskiego, a efektem łamigłówka lekka, łatwa i przyjemna.
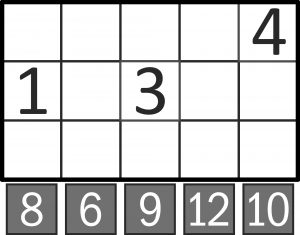
Do pustych kratek należy wpisać liczby z zakresu od 1 do 5 tak, aby:
• w każdym wierszu i w każdej kolumnie występowały różne liczby;
• suma liczb w każdej kolumnie była równa liczbie podanej u dołu w szarym polu.
Jako się rzekło, zadanie jest łatwe, więc dla tęższych głów pytanie dodatkowe: czy zbiór wszystkich ujawnionych na początku liczb w tym zadaniu – a więc nie tylko trzech w kawałku kwadratu łacińskiego, ale także pięciu sum u dołu – jest zbiorem krytycznym? Inaczej mówiąc, czy którąś (któreś?) z tych liczb można usunąć, a rozwiązanie nadal będzie tylko jedno?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Samo wpisanie liczb to faktycznie zadanie (jak na Łamiblog) ekstremalnie łatwe.
A co do pytania drugiego, to oczywiście można usunąć dowolną sumę, bo skoro „suma sum” musi być równa 45, to brakującą bez trudu da się ustalić.
5, 1, 2, 3, 4
1, 2, 3, 4, 5
2, 3, 4, 5, 1
Usunąć można dowolną z pięciu sum na dole (bo znana jest łączna suma wszystkich liczb = 45). Żadnej innej wskazówki usunąć nie można.
Rozwiązanie pozostaje jedno po usunięciu dowolnej liczby z sum co jest oczywiste. Jeżeli usuniemy dwie liczby z sum rozwiązań powstanie co najmniej dwa ze względu na zamianę kolumn z tymi sumami. Jeżeli usuniemy z sum liczby:
8 i 10 to są trzy rozwiązania zadania.
6 i 12 to jest sześć rozwiązań zadania.
6 i 10 to jest pięć rozwiązań zadania.
9 i 12 to są cztery rozwiązania zadania.
12 i 10 to są trzy rozwiązania zadania.
w pozostałych przypadkach są dwa rozwiązania
Usunięcie:
1 – powoduje, że zadanie ma 3 rozwiązania
13254 [51234] 13254
52341 [12345] 21345
21435 [23451] 52431
3 – powoduje, że zadanie ma 3 rozwiązania
51234 [21354] 21354
12345 [12435] 13245
23451 [53241] 52431
4 – powoduje, że zadanie ma 4 rozwiązania
51234 [23451] 21435 [53241]
12345 [12345] 12354 [12354]
23451 [51234] 53241 [21435]
Rozwiązanie zadania pierwotnego
21354
13245
52431
W górnej części, po usunięciu którejkolwiek z cyfr otrzymuje się co najmniej dwa rozwiązania. Natomiast zawsze można usunąć jedną, dowolną sumę – jest do wyliczenia. Próbowałem usuwać po dwie sumy: 12 i 10, a potem 6, 9 oraz 8, 6, ale również było więcej niż jedno rozwiązanie.
Myślałem, że mój komentarz (193918) o usunięciu jednej sumy był żartobliwy, ale okazuje się, że więcej usunąć się nie da. Zacznijmy od tego, że nie można usunąć 4 z górnego rzędu, bo wtedy można by było zamienić pierwszy wiersz z trzecim. Analogicznie nie można usunąć obu liczb z rzędu drugiego. Ale zarówno usunięcie 1 jak i 3, przy zostawieniu wszystkich sum, daje po kilka możliwych układów. Tak więc wszystkie trzy liczby w diagramie muszą zostać. Zostają sumy. I znowu – każda kombinacja trzech sum daje jakieś dodatkowe rozwiązanie. Wniosek – muszą zostać wszystkie 3 liczby i 4 sumy.
51234
12345
23451
W kwestii zbioru krytycznego, wygląda na to, że można usunąć dowolną z pięciu sum.
Dla spragnionych twardszego orzecha w podobnym stylu:
https://penszko.blog.polityka.pl/2012/06/23/cyfrowanka/
Bo pamięć, bo pamięć nie ta…
mp
Łatwa część rzeczywiście łatwa:
51234
12345
23451
nad trudną pomyślę 🙂
Pozdrawiam,