180 sum
Poprzedni wpis był nieco niefortunny. Położyłem nacisk na wydłużanie ciągu, co preferowało programistów i w ogóle jest sprawą drugorzędną. Uciekło mi natomiast to, co najistotniejsze: sposób szukania ciągu „na piechotę”, a ściślej – na logikę. Tak więc samo zadanie było i pozostaje ciekawe:
znaleźć ciąg rosnący złożony z kwadratów, w którym suma każdych dwu kolejnych (sąsiednich) wyrazów będzie kwadratem.
Szkopuł w tym, że końcowe pytanie nadało mu formę pasującą raczej do „Projekt Euler” niż do Łamibloga. Co prawda takie „Eulerowskie” przegięcie zdarzało mi się już nieraz, ale tym razem było przesadne. Dopowiem tylko, co zresztą wielu z Państwa zapewne zauważyło, że szukając ciągu na piechotę najwygodniej jest skorzystać z odpowiednio przekształconych wzorów na trójki pitagorejskie. W tym kontekście ciekawsze jest szukanie jak najdłuższego ciągu w minimalnym zakresie, czyli rosnącego najwolniej.
Dzisiejszy temat zacznę od trzech obrazków:
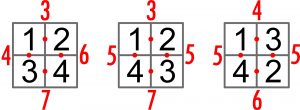
W pola kwadratu 2×2 wpisane są liczby od 1 do 4 na trzy sposoby, czyli wszystkie możliwe (z dokładnością do obrotów i odbić lustrzanych). Czerwone liczby oznaczają sumy czarnych w sąsiednich kratkach (wspólny bok). Ostatni obrazek, czyli trzeci sposób wpisania liczb wyróżnia się tym, że największa z czterech czerwonych sum jest najmniejsza – równa 6.
Zwiększamy format i wpisujemy liczby od 1 do 100 do stu pól kwadratu 10×10 tak, aby największa z sum par liczb w sąsiednich kratkach była najmniejszą możliwą. Jaka będzie ta suma?

Komentarze
Układ o roboczej nazwie „Homogenizowana Szachownica” daje wynik 106.
1 100 2 99 3 98 4 97 5 96
95 6 94 7 93 8 92 9 91 10
11 90 12 89 13 88 14 87 15 86
85 16 84 17 83 18 82 19 81 20
21 80 22 79 23 78 24 77 25 76
75 26 74 27 73 28 72 29 71 30
31 70 32 69 33 68 34 67 35 66
65 36 64 37 63 38 62 39 61 40
41 60 42 59 43 58 44 57 45 56
55 46 54 47 53 48 52 49 51 50
Liczba 106 wydaje się niezłym kandydatem na najlepszą sumę. Upakowałem liczby tak, jak pokazują strzałki:
http://pokazywarka.pl/180sum/
Są jeszcze małe rezerwy w prawym górnym i lewym dolnym rogu (sumy spadają do 102), nie widzę jednak magicznego sposobu, aby je wykorzystać.
170
Czy chodziło o zewnętrzne rzędy i kolumny? Czy trzeba było wziąć pod uwagę każdy rząd i każdą kolumnę?
Jak wynika z tytułu (180 sum) – każdy.
mp
Co najmniej jeden z rozwiązujących zadał sobie pytanie:
„A jaką najmniejszą możliwą wartość mielibyśmy na torusie?” (dochodzą sąsiedztwa pierwszej kolumny z ostatnią oraz górnego wiersza z dolnym), czyli 200 sum.
Chyba mam problem ze zrozumieniem. 10 rzędów i 10 kolumn to 20 sum, a nie 180 – gdzie jest reszta, której nie widzę?
Suma wszystkich 100 liczb to 5050, czyli na 1 rząd/kolumnę statystycznie wypada 505.
Pani Olu, chodzi o styki par kratek w rzędach i kolumnach (takie, jak te z czerwoną kropką na przykładowym rysunku) – i uwzględnia się sumy liczb w tych parach kratek. Takich styków, a więc i sum, jest 180.
mp
Czyżby 106?
Wpisałem 100 w lewy górny róg planszy i potem poszło już szybko.
Mój sposób wpisywania kolejnych liczb można łatwo odczytać z załącznika:
https://zapodaj.net/9835beee5b5a6.jpg.html
Największa suma to np 84+22 = 106. Powtórzy się ona kilka razy, ale większej nie znajdziecie. Czy mam rację?
Tak
mp
@apartado
Zadanie jest rozwojowe. Kolejne pytania mogą dotyczyć sum na skosach (400), a idąc jeszcze dalej – dlaczego ograniczać się tylko do sum dwóch sąsiednich pól? 😛
Jeśli chodzi o pytanie co najmniej jednego rozwiązującego (200), to mam obecnie wynik 117 i widzę, że 114 jest chyba osiągalne. Będę jeszcze próbował, choć w przeciwieństwie do zadania głównego, nie widzę tu tak wyraźnego schematu postępowania.
Dobry wieczór,
wydaje mi się że minimum to 106
Pozdrawiam,
Dziękuję za wyjaśnienie 🙂 Proponuję wynik 106:
http://pokazywarka.pl/0yh3e4/
@ xswedc
O torusie:
Wyczuwam ponadprzeciętne zdolności analityczne, gdyż domniemane 114 jest wynikiem, który wyrzucił mój „wyluzowany” program („wyluzowany” , więc bez pewności, że jest to minimum).
Przy okazji:
Wpadł mi dziś w ręce Omnibus Wakacyjny, więc nie będę wnikał jakie minimum wyszłoby na wstędze Möbiusa („obrócone” sąsiedztwo dwóch krawędzi).
@apartado
Wstęga Möbiusa została odkryta i wykorzystana w praktyce (!!!) co najmniej 150 lat przed narodzeniem się Möbiusa… Dokonał tego J. S. Bach, komponując sprytny i bardzo matematyczny utwór:
http://www.matematyka.wroc.pl/doniesienia/czy-bach-wynalazl-wstege-moebiusa
Filmik prezentujący ideę jest pod koniec strony, ale warto najpierw przeczytać tekst. Jest tam też link do fraktalnej strony autora.
Jeśli chodzi o „Torus im. apartado”, to bez pomocy komputera:
http://pokazywarka.pl/torus113/
Zaczyna być wyraźnie widoczna reguła, która może doprowadzić do 112, jednak ja się zadowolę wice-optymalnym wynikiem.
Ponieważ torus wprowadził sporo zamieszania do mojego życia, a potem apartado próbował mnie dobić wstęgą Möbiusa, to pomyślałem o wielowymiarowej kontynuacji w postaci butelki Kleina – w rzeczywistości nie może istnieć, a w takim zadaniu można ją jednak bezproblemowo zrealizować.
Popatrzyłem też na diagramy sklejania krawędzi tych tworów i uzupełniłem o dwa dodatkowe przypadki, coś w rodzaju butelka Kleina +:
http://pokazywarka.pl/powierzchnie/
Chodzi mi o to coś z dolnych obrazków 4 i 5. Czy te obiekty mają jakieś nazwy, właściwości, wymiary? Może jakiś link do poczytania?
https://pl.wikipedia.org/wiki/P%C5%82aszczyzna_rzutowa_rzeczywista
mp