Włącz dwa kolory
Jeśli narysujemy pięciokąt i poprowadzimy w nim wszystkie przekątne, to powstanie graf pełny, którego symbolem jest K5, co oznacza pięć punktów (wierzchołków), z których każdy połączony jest odcinkiem (krawędzią) z każdym innym. W takim grafie każdą krawędź można zabarwić jednym z dwu kolorów tak, że nigdzie nie powstanie jednobarwny trójkąt (trzy boki w tym samym kolorze). Uwzględniamy tylko trójkąty, których bokami są przekątne i boki wielokąta, a więc tylko całe odcinki łączące wierzchołki grafu.
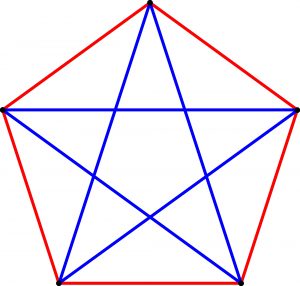
Jeśli w analogiczny sposób postąpić z sześciokątem, tworząc najpierw pełny graf K6, a potem używając dwóch kolorów do oznaczenia jego 15 krawędzi, to uniknięcie jednobarwnych trójkątów nie będzie możliwe. Ile krawędzi takiego grafu trzeba usunąć, aby dwukolorowy graf nie zawierał monochromatycznych trójkątów?
A czy ktoś potrafi ustalić, ilu krawędzi trzeba pozbawić graf pełny K10, aby przy dwóch kolorach wszystkich (45) krawędzi nie było w nim trójkątów w jednym kolorze? Wbrew pozorom odpowiedź jest zaskakująco skromna i można do niej dotrzeć na logikę.
![]()

Komentarze
Dla n-kąta (n>5) z każdego wierzchołka wychodzi k=n-1 krawędzi.
Wszystkich krawędzi jest więc K=0,5*n*(n-1). Warunkiem koniecznym* nieistnienia jednokolorowych trójkątów jest ograniczenie liczby wychodzących krawędzi do z=4 (dla z>=5 musi powstać trójkąt). Czyli z każdego wierzchołka należy usunąć u=k-z=n-5 krawędzi. Więc wszystkich krawędzi należy usunąć U=0,5*n*u=0,5*n*(n-5) (0,5 bo każdy kij ma dwa końce). Postanie nieusuniętych: Z=K-U=2n krawędzi.
_n_ __K_ __U_ _Z_
__5 __10 ___0 _10
__6 __15 ___3 _12
__7 __21 ___7 _14
__8 __28 __12 _16
__9 __36 __18 _18
_10 __45 __25 _20
100 4950 4750 200
*Warunek zapewnia, że z każdego wierzchołka można wyprowadzić nie więcej, niż 2 krawędzie w jednym kolorze. Ale nie zapewnia, że dla każdego n-kąta jest to możliwe. Przydałby się dowód…
Warunek, który poprzednio sformułowałem jest poprawny jedynie dla grafu ze wszystkimi krawędziami… Więc, jak pisał klasyk – na drugi rzut oka:
http://pokazywarka.pl/dwa_kolory/
Liczba usuniętych krawędzi = n-5
Dla K6 wystarczy usunąć jedną krawędź.
Dla K10 wystarczy usunąć pięć krawędzi (zaiste zaskakująco skromna ta odpowiedź).
Bez kartki, bez ołówka, patrząc intensywnie na graf K10 i kolorując w głowie jego krawedzie, wydaje mi się, że wystarczy usunąć 5 krawędzi.
Wszystkie usuwane krawędzie powinny być rozłączne wierzchołkowo.
Jeśli czas pozwoli, to dorzucę stosowny rysunek i parę słów opisu, jak doszedłem do wyniku
Czy Gospodarz puści to przed środą?
Pewne przyjęcie odbywało się w sali o kształcie krzyża:
http://pokazywarka.pl/bal/
Goście gromadzili się w różnych jej częściach, ale widzieli innych tylko na przestrzał, tak jak pokazują strzałki, a przykładowe rozmieszczenie gości pokazują czerwone kropki.
Ilu najwięcej gości może przybyć na to przyjęcie, aby wśród wzajemnie widzących się osób nie było trojga (lub więcej) znajomych oraz nieznajomych? Jakie będzie ich rozmieszczenie? Żadna część sali nie jest pusta.
Dla K6 wystarczy usunąć jedną krawędź (rysunek tu: https://app.box.com/s/t3qxmkv4oiwe46qdwbzto6vxxyp14hb3)
najłatwiej zacząć od K5, dołożyć wierzchołek i łączyć go unikając trójkątów.
Dla K7 bez 3 krawędzi też się da pokolorować.
Dla N-kąta z przekątnymi (N≥4) mamy „N nad 3” (symbol Newtona) możliwych trójkątów wierzchołkowych, tworzących 3 rodziny:
R2 – N trójkątów opartych na 2 sąsiednich bokach wielokąta (red) i 1 przekątnej (blue),
R1 – N*(N-4) trójkątów opartych na 1 boku wielokąta i 2 przekątnych,
R0 – pozostałe trójkąty oparte wyłącznie z przekątnych tj. jednobarwne.
Wydaje mi się, że przemalowywanie przekątnej blue na red – zamiast jej usuwania – nic nie da , bo popsuje jakiś trójkąt z R2 więc za to trzeba będzie wyrzucić krawędź red.
Wobec tego dla danego N wystarczy zbadać tylko trójkąty jednobarwne z R0 i określić minimalną liczbę L(N) krawędzi, których usunięcie wystarcza do przerwania wszystkich tych trójkątów. W tym celu można zakodować wierzchołki wielokąta cyframi i utożsamić trójkąt z trójką cyfr ABC – bez rysowania krawędzi.
Analiza po łebkach doprowadziła mnie do wniosków (oby nie pochopnych):
L(4) =0; L(5) =0; L(6) =2; L(7) =4; L(8) =6; L(9) =9; L(10) =13; …
Rozwiązanie mojego zadania z gośćmi i krzyżem.
Ponieważ Gospodarz w głównym zadaniu zahaczył delikatnie o bardzo seksowne twierdzenie Ramseya:
https://pl.wikipedia.org/wiki/Twierdzenie_Ramseya
pozwoliłem sobie rozwinąć tę ideę.
Zgodnie z tym twierdzeniem ani w poziomie, ani w pionie nie może być więcej, niż pięciu gości. Maksimum uzyskujemy, rzecz jasna, dla jednego gościa w centralnej części sali. Wtedy, w skrajnych pomieszczeniach musi być układ albo 2-2, albo 3-1. Daje to w sumie np. (1)+(2+2)+(3+1)=9 osób. Przy dwóch osobach w centrum, w skrajnych częściach muszą być układy 2-1, co daje tylko (2)+(2+1)+(2+1)=8 osób. Przy trzech osobach w centrum, w skrajnych częściach muszą być układy 1-1, co daje (3)+(1+1)+(1+1)=7 osób.
To oznacza, że wariant z jedną osobą w centrum i max. 9 gośćmi jest rozwiązaniem. Rysunek, może niezbyt czytelny, ale po krótkiej wpatrzenio-analizie, osobno w piony, osobno w poziomy, powinien być jasny:
http://pokazywarka.pl/bal_rozwiazanie/
@Markoniusz czyli medytacji wiejskiego listonosza ciąg dalszy…
Trójkąty w zbiorze R0 charakteryzują się tym, że nie zawierają wierzchołków sąsiednich. Jeśli dziesiąty wierzchołek zakodować zerem, to R0 dla N=10 zawiera 50 nast. trójkątów:
135, 136, 137, 138, 139, 146, 147, 148, 149, 157, 158, 159, 168, 169, 179, 246, 247, 248, 249, 240, 257, 258, 259, 250, 268, 269, 260, 279, 270, 280, 357, 358, 359, 350, 368, 369, 360, 379, 370, 380, 468, 469, 460, 479, 470, 480, 579, 570, 580, 680
Gdy dokładnie policzyć, wystarczy usunąć 12 krawędzi:
13, 14, 15, 24, 25, 35, 60, 68, 69, 70, 79, 80
aby rozerwać wszystkie powyższe trójkąty, czyli L(10) = 12