Licha

Sprzężenie zwrotne było na łamiblogowej tapecie przynajmniej raz, a być może więcej razy, ale na małą skalę, jakby przy okazji. Chodzi o zadania, w których występuje zależność między dwiema różnymi cechami tych samych elementów. Ściślej: obie te cechy stanowią nawzajem względem siebie zarówno przyczynę, jak i skutek. Elementami są zwykle liczby, a cechami ich liczby i wartości. Poniższe zadanie jest jeszcze jednym przykładem takiego feedbacku.
W puste pola należy wpisać takie cyfry, aby cyfra w każdej kratce oznaczała liczbę sąsiednich kratek z cyfrą nieparzystą (zwaną dawniej lichem – stąd tytuł wpisu). Sąsiednimi są kratki, stykające się bokiem lub tylko rogiem.

Przykład

Zadanie

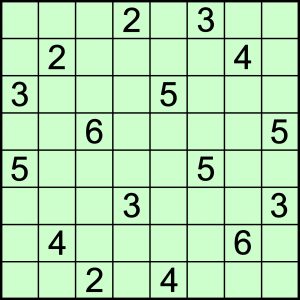
W rozwiązaniu wystarczy podać liczbę cyfr (liczb) nieparzystych w polach na przekątnych diagramu.

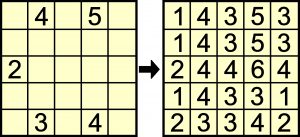
Komentarze

[OlaGM]

Pierwszy rząd to 00023320 – tak czułam już przed rozwiązywaniem, że będzie gdzieś zero 😉
Po dwie nieparzyste na każdej przekątnej: 3, 1 i 3, 1.

[apartado]

Liczba cyfr (liczb) nieparzystych w polach na przekątnych diagramu to 4.
Kapitalny początek – zapowiadała się fascynująca batalia, ale po chwili zrobiło się wręcz trywialnie – wiosną tak to się właśnie dzieje.

[Markoniusz]

diagonala (z góry na dół):
0; 2; 4; 3; 6; 6; 6; 1
2-ga przekątna (z dołu do góry):
1; 4; 4; 3; 6; 6; 4; 0

Uwagi. Oczywiście trzeba zacząć od brzegowych 5-tek, potem ustalać /nie-/parzystości pól wstawiając najmniejszą wartość i zwiększając ją gdy trzeba. Później już idzie samo jak pandemia.

[Markoniusz]

PS. http://pokazywarka.pl/i9ty3k/

[logi]

Na przekątnych są w sumie 4 liczby nieparzyste, na jednej 1 i 3 i na drugiej 1 i 3.

[Witman]

4

[grgkh]

Na obu przekątnych są po dwie liczby nieparzyste.
{{0,2,4,3,6,6,6,1},{0,4,6,6,3,4,4,1}}
Oprócz „licho” warto wspomnieć, że parzyste liczby dawniej nazywano „cetno”.

[piteren]

4

0 0 0 2 3 3 2 0
2 2 2 4 5 5 4 2
3 3 4 3 5 6 5 3
5 5 6 3 6 5 7 5
5 5 6 3 6 5 7 5
3 3 4 3 5 6 5 3
4 4 4 4 5 5 6 4
1 1 2 1 4 3 3 1

[Spytko z Melsztyna]

Jedyne rozwiązanie:
0,0,0,2,3,3,2,0
2,2,2,4,5,5,4,2
3,3,4,3,5,6,5,3
5,5,6,3,6,5,7,5
5,5,6,3,6,5,7,5
3,3,4,3,5,6,5,3
4,4,4,4,5,5,6,4
1,1,2,1,4,3,3,1
Najpierw ustalamy parzystość pól a w drugim przejeździe wpisujemy liczby.

[tomash]

Ale fajna zagadka… 🙂
Jedyne zaskoczenie to pola z cyfrą 0

Na każdej przekątnej są po dwie nieparzyste (3,1) (3,1)

[aps1968]

Od góry:
00023320
22245542
33435653
55636575
55636575
33435653
44445564
11214331
Czyli na przekątnych liczb nieparzystych po dwie.

[jukka2003]

Wyszło mi 4.

[Spytko z Melsztyna]

Jedyne rozwiązanie:
0,0,0,2,3,3,2,0
2,2,2,4,5,5,4,2
3,3,4,3,5,6,5,3
5,5,6,3,6,5,7,5
5,5,6,3,6,5,7,5
3,3,4,3,5,6,5,3
4,4,4,4,5,5,6,4
1,1,2,1,4,3,3,1

możemy otrzymać startując z 9 pięcioelementowych zbiorów krytycznych:

0,0,0,0,0,0,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,6,0
0,0,0,0,4,0,0,0
1
0,0,0,0,0,0,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0
0,4,0,0,0,0,0,0
0,0,0,0,4,0,0,0
2
0,0,0,0,0,0,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,3
0,0,0,0,0,0,0,0
0,0,0,0,4,0,0,0
3
0,0,0,0,0,0,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,5,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,6,0
0,0,0,0,0,0,0,0
4
0,0,0,0,0,0,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,5,0,0
0,0,0,0,0,0,0,0
0,4,0,0,0,0,0,0
0,0,0,0,0,0,0,0
5
0,0,0,0,0,3,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,6,0
0,0,0,0,0,0,0,0
6
0,0,0,0,0,3,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0
0,4,0,0,0,0,0,0
0,0,0,0,0,0,0,0
7
0,0,0,2,0,0,0,0
0,0,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
5,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,6,0
0,0,0,0,0,0,0,0
8
0,0,0,2,0,0,0,0
0,2,0,0,0,0,4,0
0,0,0,0,0,0,0,0
0,0,6,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,0,0
0,0,0,0,0,0,6,0
0,0,0,0,0,0,0,0
9

W poniższej tabelce w pierwszym wierszu to liczby z diagramu wypisane w kolejności od lewej do prawej i od góry do dołu.
Właśnie w tym momencie zauważyłem, że pominąłem dwie liczby z diagramu: 3 z (3,1) oraz 5 z (4,8).
No cóż przyjmijmy, że cała ta analiza dotyczy właśnie takiego okrojonego diagramu.
0 – oznacza, że dana liczba jest w zbiorze krytycznym a 1, że jej tam nie ma.
Ładnie widać, że niektóre liczby są w każdym lub prawie każdym ZK a niektóre nigdy lub prawie nigdy tam nie wpadają.

2,3,2,4,5,6,5,5,3,3,4,6,2,4
1,1,0,0,1,0,1,1,1,1,1,0,1,0
1,1,0,0,1,0,1,1,1,1,0,1,1,0
1,1,0,0,1,0,1,1,1,0,1,1,1,0
1,1,0,0,1,0,1,0,1,1,1,0,1,1
1,1,0,0,1,0,1,0,1,1,0,1,1,1
1,0,0,0,1,0,1,1,1,1,1,0,1,1
1,0,0,0,1,0,1,1,1,1,0,1,1,1
0,1,1,0,1,0,0,1,1,1,1,0,1,1
0,1,0,0,1,0,1,1,1,1,1,0,1,1

Czteroelementowych zbiorów krytycznych nie ma.
Dwa najlepsze z nich dają po 2 rozwiązania.

Jestem ciekaw czy da się ręcznie znaleźć rozwiązanie startując ze zbioru krytycznego.
Nawet nie próbowałem 🙂