Tu się zgina
Kartka papieru jest najczęściej formatu A4, czyli ma wymiary 210×297 mm. Potraktujemy ją jak prostokąt ABCD i zegniemy na pół, ale w nietypowy sposób – tak, aby punkt B pokrył punkt D. W efekcie powstanie figura taka, jak na rysunku.
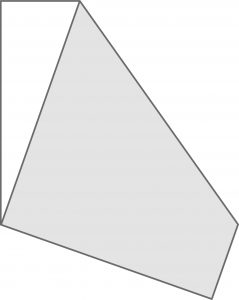
Po rozłożeniu kartki linia zgięcia będzie dobrze widoczna:
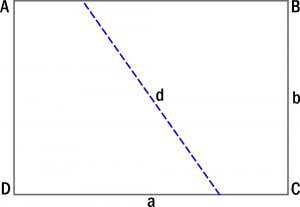
Jaka jest długość tej linii?
Chodzi oczywiście o znalezienie wzoru na długość linii zgięcia (d) w zależności od wymiarów kartki (a×b), a nie o zastosowanie metody mojego wnuka, który sięgnął po linijkę i odczytał wymiar.
To była prostsza połowa powtórki z matematyki. Druga część wydaje się nieco trudniejsza: proszę obliczyć pole powierzchni składki na pierwszym rysunku, czyli pięciokąta obejmującego części szarą i białą.

Komentarze
Dane: a, b
Szukane: d, P (zacieniowane)
Rysunek:
http://pokazywarka.pl/hsbgvz/
———————————————————————-
c liczymy z Pitagorasa:
c = sqrt{a^2+b^2}
d liczymy z podobieństwa trójkątów DCB i DEF (obydwa są prostokątne i mają kąt alfa)
0,5c : a = 0,5d : b
d = (bc) : a
d = [b x (sqrt{a^2+b^2})]:a
Zacieniowane pole to różnica pól prostokąta ABCD i trójkąta DGF. Trójkąt DGF to połowa rombu DGEF.
P (rombu DGEF) = 0,5cd
P (rombu DGEF) = 0,5 x sqrt{a^2+b^2} x [[b x (sqrt{a^2+b^2})]:a]
P (trójkąta DGF) = 0,25 x sqrt{a^2+b^2} x [[b x (sqrt{a^2+b^2})]:a]
P (zacieniowane) = ab – 0,25 x sqrt{a^2+b^2} x [[b x (sqrt{a^2+b^2})]:a]
Do upraszczania tych wyrażeń nie mam już głowy… 🙂
Ale tok myślenia chyba jest OK?
d=(b/a)*pierwiastek(a*a+b*b)=257,19204931251
P=b(3*a*a-b*b)/(4a)=38982,0454545455
Pkt. X końca linii zagięcia na odc. [AB] spełnia war. XD=XB. Oznaczając x=AX mamy z trójkąta prostokątnego AXD:
x^2+b^2 = (a-x)^2 skąd x = (a^2-b^2)/2a
Biały trójkąt czyli AXD ma pole:
P1 = xb/2 = b(a^2-b^2)/4a
Cały 5-kąt składki można rozłożyć na 4 trójkąty prostokątne (w tym 2 przystające do AXD) więc jego pole wynosi:
P = 3P1+P2 gdzie P2 = b(a-2x)/2 = b^3/2a
Ostatecznie szukane pole to:
P = b(3a^2-b^2)/4a
Można sprawdzić ten wynik dodając do P pola dwóch trójkątów zakrytych składką – powinniśmy dostać pole całego prostokąta:
P+P1+P2 = b(3a^2-b^2)/4a + b(a^2-b^2)/4a + b^3/2a = ab
Podaję odpowiedź, bez uzasadnienia (może później znajdę na nie czas):
d = (b / a) * sqrt(a^2 + b^2)
d=b/a sqrt(a^2+b^2)
P=b/(4a)(3a^2-b^2)
S = 5/8 *a *b
d=√(a^2/4+b^2 )
Dałem nadmiarową ilość nawiasów, żeby nie było żadnych wątpliwości.
d=(√(a^2+b))/a
S=?
Przyjmijmy, że dłuższa przekątna prostokąta to: p
Wtedy:
d = p*(b/a)
S = b/2*(2a-p^2/(2a))
Chyba wystarczy „przekątna” (bez „dłuższa”)
mp
Nazwijmy punkty leżące na końcach zgięcia X (na odcinku AB) i Y.
X leży w tej samej odległości od B i D, tak samo Y od A i C, więc XBYD jest rombem.
s = |AX|
t = |XB| = |XD|
s+t = a
t^2 = s^2 + b^2
Po przekształceniach:
s = a/2 – b^2/2a
t = a/2 + b^2/2a
Zacznijmy od drugiego pytania. Pole pięciokąta jest równe polu kartki pomniejszonego o połowę pola rombu XBYD.
Pole kartki, to pole rombu i dwa pola trójkątów AXD.
P(XBYD) = t*b
P = P(ABCD) – P(XBYD) / 2 = a*b – t*b/2
A pierwsze pytanie:
Przekątna kartki:
z = |BD| = √(a^2 + b^2)
P(XBYD) = d*z/2
d = 2*t*b / z
„Pole kartki, to pole rombu i dwa pola trójkątów AXD.” – to zdanie zrobiło się zbędne w momencie, gdy zmieniłem koncepcję. Zmieniła mi się też koncepcja na odmianę tego wyrazu: „pomniejszonego”.
Dla dowolnego prostokąta:
d = √(b^2+b^4/a^2)
S = (3 a^2 – b^3)/4a
Jeżeli kartka jest znormalizowanym arkuszem, to a = b √2 i wtedy:
d = b √(3/2)
S = 5√2/8 b^2
Ups, ale gafa.
Podczas rozwiązywania, pojawił mi się na rysunku romb, którego przekątnymi są długość zgięcia d i przekątna prostokąta. Chyba przez to, tak mi się głupio napisało.
Podam same odpowiedzi;
d=(b/2a)*sqrt(a^2+b^2),
s=(b/2a)*(a^2+b^2).
Pozdrawiam.
I znowu odpowiedź bez uzasadnienia:
P = (1/4) * (b/a) * (3a^2 – b^2)
Po podstawieniu danych z treści zadania, czyli standardowych wymiarów kartki A4 (podanych w milimetrach) otrzymujemy:
d = 257,1920493 mm
P = 38982,04545 mm^2
d^2=b^2 + (b^2/a)^2;
Zapomniałem o drugiej części pytani:
P=ab – (a^2+b^2)*b/(4a)