Koluśka
Najpierw narysowałem trójkąt równoboczny. Następnie wpisałem weń okrąg. A potem zaroiło się od okręgów. Kolejne były coraz mniejsze – wciśnięte w każdy róg trójkąta, styczne do ramion kąta i okręgu oczko większego. Teoretycznie ciąg małych kółeczek mógłby być kontynuowany w nieskończoność. Przypomina to słynne paradoksy Zenona, czyli bezskuteczną pogoń Achillesa za żółwiem lub strzałę nieustannie zmierzającą do celu. Próbowałem rysować te kółeczka dotąd, aż grubość okręgu zrównała się z jego promieniem, czyli kółeczko stało się kropką. Całość skojarzyła mi się z najprostszymi fraktalami. W końcu postanowiłem wrócić do geometrii.
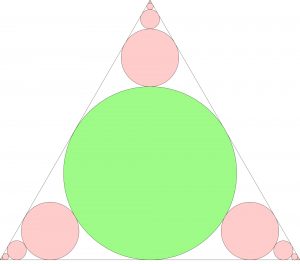
Obliczenie, jaką część powierzchni trójkąta równobocznego stanowi powierzchnia wpisanego weń okręgu, a właściwie koła – to standard. Wynik jest liczbą niewymierną. Natomiast stosunek powierzchni zajętej przez wszystkie nieskończenie liczne różowe kółka do powierzchni zielonego giganta to liczba wymierna. Jaka?
![]()

Komentarze
Niech pole zielonego giganta wynosi 1.
Liczymy sumę pól różowych kół zbiegających tylko do jednego wierzchołka trójkąta.
Okrąg wpisany w trójkąt równoboczny ma promień 3 razy krótszy, niż wysokość trójkąta. Zatem największe z różowych kół jest wpisane w trójkąt odcięty z narożnika oryginalnego trójkąta tak, aby jego wysokość była 3 razy mniejsza. Zatem pole tego największego z różowych kół to 1/9.
Każde kolejne różowe koło (wnioskujemy analogicznie) 9 razy mniejsze pole.
Zatem w jednym narożniku trójkąta różowe pola mają następującą średnicę: 1/9 + 1/27 + 1/243 + … + 1/(i^n) + …
Co zgodnie ze wzorem na sumę nieskończonego ciągu geometrycznego daje:
a1 / (1-q) = 1/9 / (1-1/9) = 1/9 / 8/9 = 1/8
Zatem wszystkie różowe koła mają pole 3 * 1/8 = 3/8, co też jest stosunkiem sumy pól różowych elementów do pola zielonego giganta.
Odpowiedź: szukany stosunek to 3/8
A co jest zielone (oprócz mnie)?
A teraz?
mp
3/8
Teraz kolor jest zielony jak się patrzy 🙂
Wyszło mi 3/8.
Każde kolejne kółko ma promień 3 razy mniejszy od poprzedniego, czyli pole 9 razy mniejsze. Jeśli przyjąć, że jest to szereg geometryczny nieskończony o pierwszym wyrazie 1/9 i ilorazie 1/9, to można policzyć jego sumę – wynosi ona 1/8. Mamy 3 takie zestawy różowych kółek, zatem razem zajmują one powierzchnię 3/8.
Po wyliczeniu z sumy szeregu geometrycznego wyszedł mi wynik 3/8, czyli 0.375 .
Promień zielonego koła to 1/3 wysokości dużego trójkąta. Stąd łatwo wynika, że rysując styczną do zielonego i największego różowego koła, odcinamy trójkąt o 3-krotnie krótszym boku, zatem promienie kół tworzą ciąg geometryczny o postępie 1/3, a pola – o postępie 1/9. Szukana proporcja to (3*1/9/(1-1/9))/1 = 3/8.
Promień zielonego koła, to 1/3 wysokości trójkąta. Trójkąt „stojący” na tym kole, czyli opisany na największym z różowych kółek, ma również wysokość równą 1/3 wysokości dużego trójkąta. Jeśli pole tego różowego koła (P = 1/9 Z – pola zielonego koła) weźmiemy za pierwszy wyraz szeregu geometrycznego, a za kolejne wyrazy pola stycznych z nim mniejszych kół, to sumą będzie: S = P / (1-q) = 9/8 P. Tych szeregów mamy trzy, więc ostatecznie:
3*S / Z = (3*9/8 P) / 9 P = 3/8
Oj… Czytałem ten wpis kilka razy i już mialem się czepiać, że powierzchnia okręgu to zawsze zero, ale tuz Przed wysłaniem komentarza zauwazylem ”
a właściwie koła”
Pisze zatem, aby uświadomić nieświadomych,, że okrąg to tylko brzeg koła i nie ma żadnej powierzchni! 🙂
Każde coraz mniejsze kółko ma promień 3 razy mniejszy niż promień poprzedniego.
Zakładamy sobie, że promień zielonego to 1.
Liczymu więc sobie sobie sume ciągu geometrycznego o współczynniku 1/9 i wyrazie początkowym 1/9 co dame nam 1/8.
No i mnożyyu jeszcze przez 3 bo tyle jest ciągów kółek.
Daje nam to więc ostatecznie 3/8.
Koluśka rozwiązanie
Promień największego różowego koła -r.
Przez punkt styku koła zielonego i różowego prowadzimy prostą
równoległą do podstawy trójkąta równobocznego. Otrzymujemy
Trójkąt podobny do dużego trójkąta zawieszony na górnym
wierzchołku. W trójkącie równobocznym promień koła wpisanego
jest równy 1/3 wysokości trójkąta. Skala podobieństwa po każdym kroku takiej operacji wynosi 1/3. Pola powierzchni maleją w każdym kroku proporcjonalnie do kwadratu skali podobieństwa. Iloraz ciągu geometrycznego pól powierzchni kół jest 1/9. Granica ciągu geometrycznego wynosi ;
a1=pi*r*r
S=pi*r*r/(1-1/9)=pi*r*r*9/8, mamy trzy takie ciągi więc suma
powierzchni kół różowych jest
3*pi*r*r*9/8=27/8*pi*r*r.
Koło zielone ma powierzchnię
pi*(3r)^2=9pi*r*r.
(27/8*pi*r*r)/(9*pi*r*r)=3/8
i to jest odpowiedź.
Metoda:
„moje małe Monte Carlo”
Wynik to coś w rodzaju:
0.32989345873294758572385723857238542738472384728374…
czyli wymiernie zaokrągliłbym do:
1/3
To nie ten stosunek:)
mp
Tak na oko to będzie ze 3/8.
Nie ujawniając postaci ułamka przyznam, że „moje małe Monte Carlo” zaniżyło właściwą wartość o około 0.03 (czyli wynik był stosunkowo blisko).
3/8
3/8
Odp: 3/8
A – pole zielonego okręgu.
B – pole jednego ciągu czerwonych okręgów.
C = A + B = pole wszystkich okręgów w jednym warkoczu liczonym od największego, zielonego koła, wspólnego dla wszystkich warkoczy.
Mamy policzyć X = 3B/A.
3A + 3B = 3C /:A
3 + 3B/A = 3C/A
X = 3(C/A-1)
Q = iloraz ciągu geometrycznego warkocza
C = A/(1-Q)
X = 3(Q/(1-Q))
h – wysokość trójkąta
ro = h/3 = promień okręgu A
r1 = h/9 = promień największego czerwonego okręgu
Q = [Pi*(h/3)^2]/[Pi*(h/9)^2] = 1/9
X = 3/8
Ponieważ narozrabiałem używając zamiennie słów okrąg i koło to w ramach kary zauważę, że istnieją krzywe o niezerowej powierzchni (np. krzywa Peano) oraz powierzchnie o zerowej powierzchni (np. dywan Sierpińskiego) 🙂
Uprzejmie donoszę, że mój komentarz 192329 nie pojawił się nawet na moment po dodaniu. Pomyślałem więc, że skasowałem go przez nieuwagę w momencie wstawiania. Powtórzyłem go więc wpisem 192330 i ten wskoczył normalnie. Sprawa jest w zasadzie błaha ale już widzę pytanie do Gospodarza: Co się stało z …….? Swoją drogą mamy tu zagadkę dla informatyków 🙂
Ja sobie z tą łamigłówką nie poradzę. Chyba że… 192329 to liczba, która jest zlepkiem trzech kolejnych liczb pierwszych. Może dlatego 🙂
mp