Feedback
Od dawna przymierzam się, aby pozbierać łamigłówki, w których występuje sprzężenie zwrotne. Chodzi oczywiście o rodzaje, a nie konkretne zadania. Kiedyś wydawało mi się, że zbiorek będzie dość pokaźny, jak na tak nietypowy temat – powiedzmy kilkanaście sztuk. Potem, błądząc po aktualiach i archiwach, doszedłem do wniosku, że wręcz przeciwnie – zbierze się tylko kilka eksponatów i niemal wszystkie oparte na podobnej zasadzie, dotyczącej zależności między liczbami, jako elementami zbioru, a ich wartościami.
Zadania z feedbackiem są pomysłem stosunkowo nowym. Prawdopodobnie pierwszymi były tzw. liczbowe samozdania (self-referential sentences), zwane także autogramami, które polegały na uzupełnianiu zdań liczebnikami, a pojawiły się na łamach Scientific American w rubryce Metamagical Themas Douglasa Hofstadtera na początku lat 80. ub. wieku. Są one nieco ciekawsze w językach fleksyjnych, a więc głównie w polskim, bo uzupełniając liczebnikami np. poniższe zdanie trzeba pamiętać, aby było ono nie tylko prawdziwe, ale także poprawne gramatycznie:
W TYM ZDANIU JEST _______ LITER T, _______ LITERY Ś ORAZ _______ LITER I.
Sztandarowa łamigłówka ze sprzężeniem zwrotnym debiutowała w roku 1995 w japońskim magazynie Puzzler i była przez wiele lat jednym z dań firmowych tego pisma. Mimo oryginalnego, znakomitego pomysłu nie wypłynęła na szersze wody, bo należy z natury – jak zresztą wszystkie zadania ze sprzężeniem zwrotnym – do twardych orzechów. W Polsce nosi nazwę „Cyfry do strzałek”, na świecie debiutowała jako „Number Pointers”, ale pojawia się także pod innymi nazwami, np. „Japanese Arrows”. Przed wielu laty gościła w Łamiblogu (chyba nawet dwukrotnie), ale skoro szykuję mały przegląd zadań z feedbackiem, postanowiłem ją przypomnieć.
Instrukcja jest krótka i zakręcona:
do każdej kratki należy wpisać taką cyfrę X – z zakresu od 1 do 6 – aby strzałka w danej kratce wskazywała na tyle różnych cyfr, jaka jest wartość cyfry X. Na dobry początek jedna cyfra jest już na swoim miejscu.
W małym przykładzie zakres cyfr jest oczywiście odpowiednio mniejszy.
Przykład
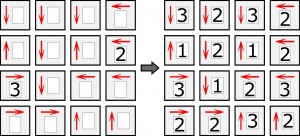
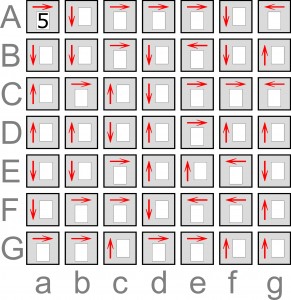
Zadanie jest ekstremalnie trudnym sprawdzianem logicznego myślenia, koncentracji i wytrwałości. Wypadałoby je opatrzyć ostrzeżeniem: do rozwiązywania na własną odpowiedzialność. Na okoliczność ewentualnych uwag, dotyczących sposobu lub toku rozwiązywania, wiersze i kolumny diagramu oznaczone są literami. Moim zdaniem na początku rozwiązywania udaje się po krótkich „bólach” ustalić cały jeden rząd. Który?
Jeśli mimo wszystko komuś uda się dotrzeć do finału, wystarczy, jeśli poda, ile razy w diagramie występują cyfry 3 i 4. Mile widziane będą także informacje o czasie rozwiązywania.

Komentarze
Zadanie 1:
sześć … dwie … sześć
Zadanie 2:
Gdyby nie ta 5-ka, zadanie byłoby trywialne 😉 wystarczyłoby wypełnić diagram jedynkami :).
Feedback niedokończony:
Dwa znaki zapytania wskazują cyfry, wskazujące błędnie.
Pomożecie?
5 >|4 V|4 >|3 >|2 >|6 V|5 |4 V|2 |1 ^|4?V|2 >|1 >|3 |2?^|3 ^|
2 V|1 V|4 >|3 ^|1 ^|4 |4 >|1 V|2 <|3 |4 >|3 ^|3 >|2 >|6 ^|5 ^|
Ciężko pomóc, bo trudno się zorientować, co przedstawia powyższy zapis.
mp
(w poprzedniej wersji były strzałki, które zepsuły formatowanie)
Feedback niedokończony:
Dwa znaki zapytania wskazują cyfry, wskazujące błędnie.
Pomożecie?
5|4|4|3|2|6|5|
4|3|4|4|2|5|1|
2|4|1|4?|2|1|3|
3|2|2|2|2|2?|3|
2|1|4|3|1|4|2|
1|4|4|1|2|3|4|
5|4|3|3|2|6|5|
Pomoc chyba nie pomoże, bo błędne cyfry są w dwudziestu kratkach.
mp
5432155
4343241
2423214
3232133
2122221
1441234
4433254
Nie wiem jak „mądrze” rozwiązać to zadanie.
Logiczne myślenie i koncentrację odłożyłem na bok, a wybrałem to czego wybrać nie powinienem – dużą wytrwałość.
5|4|3|2|1|5|5|
4|3|4|3|2|4|1|
2|4|2|3|2|1|4|
3|2|3|2|1|3|3|
2|1|2|2|2|2|1|
1|4|4|1|2|3|4|
4|4|3|3|2|5|4|
Mam cichą nadzieję, że to inne rozwiązanie niż oryginał.
Byłoby wtedy ciekawiej.
Brawo! Niestety, rozwiązanie, jak Matka, jest tylko jedno 🙂
mp
Cyfra 3 występuje 11 razy a cyfra 4 występuje 12 razy.
Poniżej rozwiązanie:
5 4 3 2 1 5 5
4 3 4 3 2 4 1
2 4 2 3 2 1 4
3 2 3 2 1 3 3
2 1 2 2 2 2 1
1 4 4 1 2 3 4
4 4 3 3 2 5 4
Co do czasu to szkoda gadać, bo rozwiązałem praktycznie na „piechotę”, a jeszcze w międzyczasie dwa programy napisałem. Niestety, nie dawały rady z ilością kombinacji i dopiero po rozwiązaniu grubo ponad połowy można było jeden z nich zastosować (chociaż z tym małym kwadratem 4×4 z przykładu radził sobie bez problemu).
Dziękuję za ciekawy komentarz – zwłaszcza za wzmiankę o programie. Podejrzewałem, że skuteczne zaprogramowanie tego zadania jest trudne.
mp
Lepiej późno niż wcale 🙂 Feedback nie dawał mi spokoju i musiałem
się z nim rozprawić choćby po terminie.
Zadanie najlepiej robi się metodą komputerowo-ręczną.
Najpierw rozprawiamy się ze sprzężeniami zwrotnymi lokalnie
czyli w każdym wierszu i każdej kolumnie oddzielnie.
W ten sposób powstają listy możliwych wierszy i kolumn.
listy te można znacznie skrócić zawężając dziedzinę dla
poszczególnych pozycji w ciągach, patrząc jakie cyfry
nie pojawiają sie w wynikach na konkretnych pozycjach
i wielokrotne puszczanie sprawdzeń dla różnych wierszy i kolumn.
Idzie to bardzo mozolnie ale po ok. 35 takich przebiegach
dostajemy dość krótkie listy możliwych wierszy i kolumn
o następujących długościach:
W1 – 1 K1 – 3
W2 – 18 K2 – 4
W3 – 6 K3 – 24
W4 – 24 K4 – 2
W5 – 6 K5 – 24
W6 – 3 K6 – 2
W7 – 9 K7 – 3
Na tym etapie mamy też ustalone 19 cyfr w tym cały pierwszy wiersz.
(Spodziewałem się że już ta procedura pozwoli znaleźć rozwiązanie
w postaci wystarczającej ilości list jednoelementowych ale niestety).
Teraz generujemy wszystkie 419904 możliwe kwadraty i sprawdzamy
czy każda kolumna w takim kwadracie da się odnaleźć w odpowiednim
zbiorze wygenerowanym w pierwszym etapie. Jeśli tak to mamy dobry kwadrat. Rzeczywiście program znalazł tylko jeden taki kwadrat. (Właśnie przed chwilą sprawdziłem że jakby te kwadraty konstruować z kolumn a nie wierszy to byłoby ich tylko 82944, ale to bez znaczenia bo komp policzył to w kilka lub kilkanaście minut – tyle trwała kolacja). Cała robota zajęła mi kilka ładnych godzin czystej pracy ale da się to zrobić programem. Robienie tego ręcznie rzeczywiście może zakończyć się pobytem w szpitalu albo przegraną co na jedno wychodzi 🙂
@ Spytko z Melsztyna
A gdyby kolumn/wierszy było powiedzmy po 8 (zamiast 7) , to czy zadanie byłoby dla komputera do „przełknięcia” czy jednak musiałby popracować o wieeeele dłużej.
Może dałoby się przy okazji poprosić Naszego Gospodarza o takie zadanie w odrobinę większym rozmiarze ? – podejrzewam, że mogłoby to mieć pozytywny wpływ na ilość feedbacków.
sześć, dwie, siedem
@ apartado:
Wydaje mi się, że w tym zadaniu rozmiar danych ma niewielkie znaczenie.
Podstawowe znaczenie ma układ strzałek.
Im więcej jest strzałek wzdłuż kierunku wiersza/kolumny tym krótsze listy.
Im więcej strzałek na kierunku wiersza/kolumny ma przeciwne zwroty tym krótsze listy.
Przy konstrukcji kwadratów po pierwszym etapie należy wybrać wiersze lub
kolumny w zależności od tego co ma mniejszy iloczyn mocy zbiorów.
Mam wrażenie, że można skonstruować złośliwy kwadrat 7×7,
który będzie się liczył dłużej niż user friendly kwadrat 10×10.
Przyłączam się do prośby do Gospodarza o takie (2, 3 rzędy większe n i
zrównoważona ilość przeciwnych strzałek) zadanie 🙂
@ Spytko z Melsztyna
Zwiększenie rozmiaru pola o 1, zwiększy zakres wpisywanych liczb o 1 (zamiast 1-6 będzie 1-7).
To wzrost ok około 16%, ale intuicja podpowiada mi, że złożoność obliczeniowa może wzrosnąć wielokrotnie.
Moja ciekawość rośnie – uśmiech skierowany w stronę Gospodarza jest teraz rzeczą naturalną 🙂
Zaryzykuję i zamieszczę większe Strzałki za tydzień.
mp
Podążyłem tropem Spytka, ale zanim dotarłem do Melsztyna, sprzęgłem się zwrotnie.
Początek identyczny:
W1 – 1 K1 – 3
W2 – 18 K2 – 4
W3 – 6 K3 – 24
W4 – 24 K4 – 2
W5 – 6 K5 – 24
W6 – 3 K6 – 2
W7 – 9 K7 – 3
Teraz wyznaczam dla każdej kratki możliwe cyfry, uwzględniając powyższe listy:
5 | 4 | 3 | 2 | 1 | 5 | 5
3,4 | 3,4 | 3,4 | 2,3 | 2,1,3 | 4,5 | 1
2 | 3,4 | 1,2 | 2,3 | 2 | 1 | 3,4
3 | 1,2 | 1,2,3 | 1,2 | 1,2 | 3,2 | 3
2 | 1,2 | 1,2,4,3 | 2 | 2,3 | 2,4 | 2,1
1 | 3,4 | 2,3,4 | 1 | 3,2 | 3 | 3,4
3,4,5 | 3,4 | 2,3,4 | 3,2 | 2,1 | 5 | 3,5,4
Daruję sobie formatowanie, ale w większości kratek jest jedna lub dwie cyfry. Tylko w siedmiu jest więcej.
W następnym kroku biorę pierwszą kratkę z niepewnością i w pętli wybieram każdą z możliwości, po czym uruchamiam algorytm od początku.
Okazuje się, że wybór złej cyfry niemal zawsze prowadzi do braku list w kolejnym kroku. Tak jest, dla pierwszej kratki w drugim wierszu: po wpisaniu 3 mamy ZONK.
Wpisanie poprawnej 4 daje:
W1 – 1 K1 – 2
W2 – 6 K2 – 3
W3 – 3 K3 – 12
W4 – 24 K4 – 2
W5 – 6 K5 – 16
W6 – 3 K6 – 2
W7 – 5 K7 – 3
I kratki:
5 | 4 | 3 | 2 | 1 | 5 | 5
4 | 3,4 | 4 | 2,3 | 3,2 | 4,5 | 1
2 | 3,4 | 2 | 2,3 | 2 | 1 | 3,4
3 | 1,2 | 1,2,3 | 1,2 | 1,2 | 3,2 | 3
2 | 1,2 | 1,2,4,3 | 2 | 2,3 | 2,4 | 2,1
1 | 3,4 | 2,3,4 | 1 | 3,2 | 3 | 3,4
4,5 | 4 | 3,4 | 3,2 | 2,1 | 5 | 4,3,5
Nie są to drastyczne zmiany, ale już na następnym etapie dostajemy końcowe rozwiązanie, gdy do drugiej kratki w drugim wierszu wpisujemy 3. Wpisanie tam 4 daje sprzeczność.
Czas działania: kilka sekund (ale kod jest daleki od optymalnego), niemal w całości w pierwszym kroku.
Algorytm wybiera pierwszą wolną kratkę do zgadywania. Ale jeśli wpisałem 1 w ostatniej kratce piątego wiersza, to rozwiązanie przyszło od razu. Na pewno w tym kroku można jeszcze wiele uzyskać przy optymalizowaniu algorytmu. Np. uzależniając wybór kratki od liczby list w wierszu i kolumnie.
Zobaczymy, jak będzie dla większej planszy.
Nie próbowałem tworzyć własnych sprzężeń, więc nie wiem, na ile typowe jest to z zadania. Być może któreś inne zwróci na tyle dużo list, że dozwolonych cyfr będzie wciąż bardzo dużo i złożoność będzie większa.
Kilkanaście lat temu napisałem w TurboBasicu program rozwiązujący Strzałki. Kilka lat temu przerobiłem go na Visual Basic, żeby wygodniej wprowadzać dane, chociaż w przypadku tego zadania i tak zajmuje to ok. 2 i pół minuty. A samo rozwiązanie trwa szybciej – jakieś 6 sekund.
Posługując się programem sprawdziłem, że same strzałki (bez cyfry 5 w lewym górnym rogu) dają 14 różnych rozwiązań (w tym oczywiście rozwiązanie trywialne z samych jedynek). Do tego, aby otrzymać takie samo rozwiązanie, wystarczy umieszczenie właściwej cyfry w jednym z pól: Ab, Ag, Ba, Bc, Da, Ga, Gb.
Jednoznaczne rozwiązanie otrzymamy też, gdy w polu Aa będzie tylko cyfra 5, bez ujawnionego kierunku strzałki.
I jeszcze ciekawostka, związana z centralnym polem Dd. Jednoznaczne rozwiązanie otrzymamy, umieszczając tam strzałkę skierowana w dowolna stronę, przy czym oczywiście kierując ją w dół, zmienimy wartość w tym polu na 3, bez zmiany jakiejkolwiek cyfry w innych polach.
Ale do rozwiązania tego zadania komputer nie jest niezbędny. Rozwiązując ręcznie, doszedłem do tego samego zestawu cyfr, który podał y-b. Od tego momentu nie daje się wprawdzie nic dalej poprawić, analizując osobno każdy wiersz czy kolumnę, ale można przyjąć jakieś założenie i po kilku krokach otrzymać sprzeczność. Poniżej schemat takiego rozwiązania:
Końcówka wiersza G może mieć postać 2155, 3254 lub 3253, a końcówka kolumny g:
133, 144 lub 245.
Jeżeli Ef=4, to Ec=4, Ee=3 i Eg=1. Z Ee=3 wynika Be=3, Bd=2, Gd=2, Gg=5 i Fg=4. Ale jest to sprzeczne z Eg=1, zatem Ef≠4 czyli Ef=2 → Bf=4 → Df=3 → De=1, a także Ec≠4
Jeżeli Ec=3, Ee=3 oraz Eg=1, to tak jak poprzednio Be=3, Bd=2, Gd=2, Gg=5 i Fg=4. Znowu mamy sprzeczność z Eg=1, więc Ec≠3.
Jeżeli Ec=1, to Ee=2 i Eg=2 → Gg=5 → Gd=2 → Bd=2 ale z Ee=2 wynika Be=2 więc Bc=3 i Ba=3 → Ga=3 i mamy sprzeczność, bo na prawo od Ga jest 4 lub 5 różnych cyfr. Zatem Ec=2
Kolumna c musi zaczynać się od 331 albo 342, więc Gc≠2
Jeżeli Gc=4, to Cc=1 → Bc=3 → Be=2 → Ba=3 → Ga=3 i znowu sprzeczność więc Gc=3
Jeżeli Ee=3, to Be=3 → Bd=2 → Gd=2 → Gg=5 → Fg=4 → Fb=4. Ale jednocześnie Gb=4, więc powinno być Eb=1, co jest sprzeczne z Ef=2.
Zatem Ee=2 → Eg=1, Eb=1, Be≠3
Z Eg=1 wynika Gg≠5 → Ge=2 → Gd=3 → Ga≠5
Z Eb=1 i Ab=4 wynika Db=2
Cd=3 → Bd=3→ Dd=2
Z analizy kolumny b wynika Fb=Gb=4 → Ga=4 i Gg=4 → Fg=4 → Cg=4 → Cb=4 → Bb=3
Z Ga=4 wynika Ba=4
Z Fb=4 i Fg=4 wynika Fe=2 i Fc=4
Dc=3
Cc=2→ Bc=4
Be=2
Koniec