Szkielet z dodatkami
Najbardziej oryginalne w arytmetyce „szkieletowej” są mnożenia lub dzielenia całkowicie pozbawione cyfr. Inaczej mówiąc, zadanie polega na rekonstrukcji zapisu działania, w którym każdą cyfrę zastępuje nic nie znaczący znak – zwykle kreska lub kratka. To trochę tak, jakby chodziło o rozszyfrowanie tekstu, gdy znane są tylko miejsca, w których znajdują się litery. Trochę, ponieważ w tekście z położenia liter nie wynikają żadne zależności między nimi. Można co najwyżej ogólnie wnioskować, że jeżeli na przykład wyraz jest 5-literowy, to gdzieś musi w nim tkwić samogłoska (o ile nie mamy do czynienia z językiem słowackim lub czeskim, w których trafiają się zdania w rodzaju Škrt plch z mlh Brd pln skvrn z mrv prv hrd scvrnkl z brzd skrz trs chrp v krs vrb mls mrch srn čtvrthrst zrn).
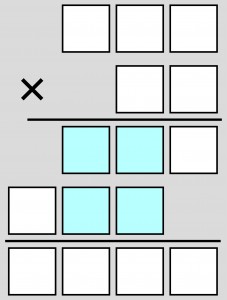
„Gołe szkielety” arytmetyczne bez żadnych dodatkowych informacji, ułatwiających rozwiązywanie, to wyjątki i zwykle twarde orzechy. W Łamiblogu pojawiły się tylko dwukrotnie: tu i tu. Natomiast znacznie częstsze są „golizny” z dodatkami – jak choćby poniższy zapis mnożenia.
Dodatki brzmią: w błękitnych kratkach powinna się pojawić taka sama cyfra, nie występująca nigdzie indziej oraz nigdzie nie może być jedynki.
I dodatkowe pytanie: czy jest jakiś sprytny sposób uporania się z tym zadaniem, czyli taki, który nie wymaga rozwiązywania po kolei ośmiu „podzadań” z konkretnymi cyframi w niebieskich polach?

Komentarze
Sprytny sposób nr 1:
Napisać program komputerowy, który przeanalizuje wszystkie możliwości. Wprawiony programista zrobi to w 5 minut i juz ma rozwiązanie 🙂
Tylko trzeba jeszcze mieć włączony komputer, a ja mam tylko w pracy włączony. W domu komputera nie ruszam 🙂
Mam prośbę o doprecyzowanie:
Czy cyfra, która znajduje się w niebieskich kratkach może pojawić się w innych miejscach diagramu.
Z przedstawionej we wpisie treści wynika, że jest to możliwe (i taką wersję przyjmuję za właściwą), ale chciałbym się upewnić, czy przypadkiem autor zadania nie zapomniał wspomnieć, że niebieska cyfra pojawia się tylko w niebieskich kratkach (co może znacznie uprościć zadanie).
Racja. Nie może. Naniosłem poprawkę.
mp
Nie ma warunku, że cyfra z niebieskich kratek nie może się powtarzać, że cyfry zadania nie powtarzają się?
Nie ma żadnych innych warunków, tylko taki, że w 4 niebieskich ma być taka sama cyfra? 222×22 na przykład spełnia warunki, 333×22 też, 222×33 oraz 333×33.
Szukałem warunku, że cyfry nie mogą się powtarzać, ale nie widzę 🙁
Słusznie. Uzupełniłem tekst.
mp
294×23
trudno mi podac jakies zlote mysli, po kilku chwilach zastanowienia widać, że lewa strona liczb musi być malutka, żeby nie powiększyć liczby cyfr wyników cząstkowych.
Sprawdzania ogranicza się dokładnie do dwóch: 2 i 3 (mam tu na myśli mnożną dwucyfrową) a co za tym idzie, szybko dochodzi się do liczby 8 w niebieskim polu.
Dokładnie drugi mój strzał był trafiony.
Przy podanych warunkach rozwiązanie jest jedno:
294
*23
——
882
588
——
6762
Rozwiązałem przy pomocy komputera. Program jest łatwy do ułożenia.
Gdyby wszystkie trzy iloczyny były 5-cyfrowe to są jeszcze dwa rozwiązania:
482*97
963*68
294*23, na niebieskim ósemki.
łatwo wyeliminować z niebieskiego 2,3 i 9. Potem pisze się program 🙂
łatwo też wyeliminowac nieparzyste (niebieskie musiałoby = 9), zostaje 4,6 i 8.
294×23=6762
Komputer mi powiedział, że działanie to 294 * 23.
Szukana cyfra to 8.
294×23 = 6762, iloczyny cząstkowe 882 (x3) i 588 (x2). Sprytny sposób: należy skupić się na dwucyfrowym mnożniku. Musi być różnocyfrowy, odpada 1, odpada oczywiście 0, a liczba trzycyfrowa większa od 200 musi po pomnożeniu przez każdą z cyfr mnożnika dać liczbę jeszcze trzycyfrową. Teoretycznie zostają więc 23, 24, 32, 34, 42, 43. To naprawdę okazuje się nie być wiele możliwości do sprawdzenia, np. czwórka na pozycji 10-tek musiałaby w wyniku mnożenia dać 988, a więc mnożną 247, co po przemnożeniu przez 2 lub 3 nie daje tego, co chcemy. Potem sprawdziłem w roli cyfry dziesiątek trójkę, na koniec wyszedł wynik dla dwójki. Ósemka na niebieskich polach była wynikiem, nie założeniem.
Znalazłem 294*23 = [882;588]= 6762
Z ośmiu „podzadań” najpierw wybrałem „6” – bez powodzenia, potem „8” i tu już z sukcesem.
„2” i „3” raczej odpadają, jeśli nie może być cyfry 1.
Ale ciekaw jestem, czy to rozwiązanie, które znalazłem jest jedyne – w wolnej chwili sprawdzę jeszcze pozostałe 4 cyfry.
2 9 4
× 2 3
8 8 2
5 8 8
= 6 , 7 6 2
Ten przecinek w iloczynie „jest symbolem mojej indywidualności i wiary w wolność jednostki”.
Sprytny sposób nr 2:
Górny czynnik to minimum 200. Dolny zatem musi mieć obie cyfry z zakresu od 2 do 4. Do tego obie cyfry różne.
To oznacza, że górny czynnik pomnożony przez 3 daje liczbę 3 cyfrowa.
Czyli górny czynnik nie przekracza 333.
Ponadto cyfra w niebieskiej klatce to minimum 4.
Sprawdzamy na siłę wszystkie wartości górnego czynnika, dla których iloczyn górnego czynnika przez 2, 3 i 4 jest postaci xxy, oraz zxx… To w sumie po ok. 20 przypadków z jednej i drugiej strony. Niby dużo, ale po chwili przemyśleń wszystkie można bez problemu wypisać z głowy.
Potem porównujemy które wpisy pasujące dla szablonu xxy pasują do szablonu zxx i otrzymujemy rozwiązanie
294 * 23
Zastanowię się czy można jeszcze jakoś zmniejszyć liczbę przypadków do rozpatrzenia, choć uważam, że marne ok. 40 wartości to i tak ładny wynik, wszystko zrobione w głowie, całość zajęła ok. 15 minut…
Działanie:
294
* 23
—————-
–882
588
—————
6762
Do rozwiązania zadania potrzebowałem tylko tablicy matematycznej dzielników liczb trzycyfrowych. Porównywałem dzielniki liczb XXi oraz iXX. (Oczywiście X oraz i rózne od 1). Gdy znalazłem takie liczby ABC*D=XXi oraz ABC*E=iXX, wówczas trzycyfrowy czynnik iloczynu wynosi ABC, zaś dwucyfrowy czynnik iloczynu wynosi ED. Należało jeszcze sprawdzić, że każda z cyfr A,B,C,D,E jest różna od 1 oraz od X. W sumie 15 minut rozwiązywania, w tym krótka konwersacja z domownikami.
Jedyne rozwiązanie:
_294
*_23
——-
_882
588_
——-
6762
A tu jest sprytny sposób:
http://pokazywarka.pl/39zta3/
Wszystkim Paniom życzę zdrowia z okazji ich święta! 🙂
Sądząc po numeracji, jest sporo poprawnych rozwiązań.
A jeszcze wyszło mi zadanie: to samo, tylko dwa „górne” pola pozostają niebieskie, a dwa „dolne” są inne, np. pomarańczowe, czyli mamy 2x po dwie takie same cyfry. Cyfra „pomarańczowa” może pojawić się w reszcie diagramu, a „niebieska” nie, cyfra „1” nie występuje tak jak w oryginale.