Różnicowo
Przypomnę, że z „sekretnym” prostokątem, którego długości boków wyrażają się liczbami całkowitymi, bywa dwojako:
– jeśli znamy jego pole, to czasem możemy ten prostokąt narysować (gdy pole wyraża się liczbą półpierwszą);
– jeśli znamy jego obwód, to prostokąta prawie nigdy nie narysujemy, chyba że obwód równy jest 4 lub 6.
Te dwa przypadki stanowią „podwaliny” goszczących w przedpoprzednim wpisie dwóch łamigłówek – shikaku i rekuto.
Ale mamy jeszcze trzecią możliwość:
– jeśli znamy różnicę długości boków prostokąta, oczywiście sąsiednich, to nie narysujemy go nigdy, bo informacja jest zbyt skąpa, chyba że miejscem akcji będzie łamigłówka sadekaku – jak wynika z nazwy, także z japońskim rodowodem:
Diagram z liczbami należy podzielić wzdłuż linii przerywanych na prostokąty – w każdym powinna się znaleźć jedna liczba, która powinna być równa różnicy długości boków tego prostokąta.
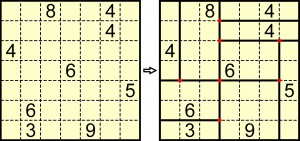
W łamigłówce shikaku z przedpoprzedniego wpisu liczby oznaczały pola, a przykład z rozwiązaniem wyglądał tak:
Gdy liczby oznaczające pola zamienimy na oznaczające różnice długości boków każdego z prostokątów – takich jak w rozwiązaniu shikaku – to powstanie sadekaku:
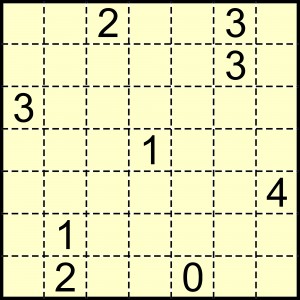
Co ciekawe, rozwiązanie tego przykładu jest także jedno i takie samo, jak wyżej. Natomiast poniżej znajduje się sadekaku dla tęgich i cierpliwych głów.
Jako rozwiązanie wystarczy podać, w ilu punktach stykają się linie dzielące diagram (w rozwiązaniu przykładu shikaku takich punktów, oznaczonych na czerwono, jest 7).


Komentarze
23, czyli: http://pokazywarka.pl/ytb2uj/
Pozdrawiam poświątecznie! 😉
Punktów, w których stykają się linie dzielące diagram jest 23.
http://pokazywarka.pl/5z1vke/
23
Linie dzielące diagram stykają się w 23 punktach.
Czas rozwiązywania: około 10 minut.
krótki opis metody:
22 krótkie odcinki wpisane jako pewniaki, a potem educated guess 😉
W 23 punktach
http://i.imgur.com/EmZTywT.png
23
A może warto pójść jeszcze dalej i spróbować przygotować miksa shikaku, rekuto i sadekaku, tzn. wersję, w której każda z liczb umieszczonych w diagramie oznacza np. pole lub połowę obwodu, albo pole lub różnicę długości boków, albo dowolną z tych trzech własności?
Obawiam się jednak, że przygotowanie jednoznacznego przykładu z tak słabą informacją jest nie lada wyzwaniem. Choć zawsze można uzupełnić niektóre liczby o informację, którą własność prostokąta opisuje konkretna liczba.
Układaczom z pewnością taki pomysł się nasuwa, ale trudno powiedzieć, czy efekt byłby strawny, a tym bardziej kuszący dla rozwiązywaczy. Spróbować oczywiście warto.
mp
Mimo, że położenie 10 prostokątów da się wydedukować, nie jest łatwo. Ostatecznie wychodzą 23 przecięcia.
Bardzo miło sie rozwiązywało po świątecznych ucztach 🙂
http://s23.postimg.org/o35cif07v/roznicowo.png
Szukając ciekawych odmian tego typu łamigłówki, rozważyłbym możliwość dodania informacji o ilości granic pomiędzy prostokątami w poszczególnych wierszach i kolumnach.
Intuicja podpowiada mi, że w tej wersji można by cyfry z wnętrza diagramu zastąpić oznaczeniami przynależności pola do osobnego prostokąta (kropka zamiast informacji o wartości).
Przyznam, że zadanie było dość trudne. Albo po prostu nie znalazłem tego czegoś, co otwiera łatwą drogę do rozwiązania 🙂
▶▷▷◀◀◀◀◁◁◁
▶▷▷◀◀◀◀◁◁◁
▶◢△△◣◣◣◣◣▽
▶◢△△◣◣◣◣◣▽
▶◢◤◤◤◤◤◸◸▽
◥◥◹◹◹◆◺◸◸▽
◥◥◹◹◹◆◺◸◸▽
◥◥◾◾◾◆◺◸◸▽
◥◥◾◾◾◆◿◿◈◈
◇◇◇◇◇◆◿◿◈◈
PS. Mam nadzieję, że rysunek będzie czytelny 🙂
Niestety nie jest 🙁
ABBCCCCDDD
ABBCCCCDDD
AEFFGGGGGH
AEFFGGGGGH
AEIIIIIJJH
KKLLLMNJJH
KKLLLMNJJH
KKOOOMNJJH
KKOOOMPPQQ
RRRRRMPPQQ