Dowiedź
Co pewien czas zastanawiam się nad różnicą między zadaniem matematycznym a łamigłówką matematyczną. Jednak właściwie nic nowego nie odkrywam – sprawa tradycyjnie sprowadza się do stwierdzenia, że różnica jest płynna i subiektywna. Jest także kwestią umowną, bo można np. przyjąć, że zadanie to proste ćwiczenie, sprawdzające i utrwalające nabytą wiedzę, a łamigłówka to coś bardziej zakręconego. Na czym polega „zakręcenie”, to temat do dyskusji, ale o tym przy innej okazji. Tymczasem doszedłem do wniosku, że RASOWE zadania matematyczne mają pewną cechę, która w łamigłówkach jest „wynaturzeniem”. Mam na myśli DOWÓD. W zdecydowanej większości takich rasowych zadań należy czegoś dowieść, natomiast końcowym efektem łamigłówki jest prawie zawsze tylko jakiś krótki tekstowy lub rysunkowy konkret.
Piszę o tym nie bez kozery. 15 listopada zamieściłem w „Na pamięć” prostą łamigłówkę, po której otrzymałem sporo maili z prośbą o… dowód.
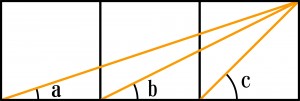
Z trzech kwadratów utworzono prostokąt, w którym następnie oznaczono trzy kąty – a, b i c. Co jest większe – kąt c czy suma kątów a i b?
Prośby o dowód mnie zaskoczyły, bo rozwiązanie sprowadza się do szkolnego wzoru z trygonometrii. Podejrzewam, że wiele osób nie pamiętało tego wzoru i szukało rozwiązania czysto geometrycznego. Takie rozwiązanie, czyli dowód, że między sumą kątów a i b oraz kątem c zachodzi określona zależność – istnieje i jest dość oryginalne, sprytne i proste. Proszę spróbować je znaleźć.

Komentarze
kąt C ma 45 stopni – chyba nie trzeba udowadniać
suma kątów A+B również ma 45 stopni – wynika to ze wzoru na sumę kotangensów.
ctg(A+B)= (ctgA * ctgB – 1) / (ctgA + ctgB)
ctgA= 3/1 = 3
ctgB = 2/1 = 2
ctg(A+B) = (3*2-1) / (3+2) = 1
więc A+B = 45 stopni
ze wzoru na cotangens sumy miało być oczywiście a nie sumę cotangensów 😉
Hmmm… dla kątów ‚a’ i ‚b’ w przedziale 0-90st zachodzi nierówność:
a>b => tg(a)>tg(b), wynika to wprost z monotoniczności funkcji tangens w interesującym nas przedziale.
W naszym przypadku mamy 1/3 + 1/2 < 1/1,
czyli 5/6<1, a więc a+b<c
Nad dowodem geometrycznym trzeba będzie się chwilkę dłużej zastanowić.
P.S. kurcze po przeliczeniu kalkulator powiedział co innego…. hmmm… suma jest równa 45st… ciekawe…
Kąt C ma 45 stopni.
Rysunek: http://www.gg.pl/dysk/lWtKQhgLCjhQlGtKQhgLGhE/dowiedz.png
Na rysunku widzimy kwadrat, którego wierzchołki umieszczono w punktach kratowych. Kąt pomiędzy niebieską przekątną kwadratu a żółtym bokiem kwadratu ma 45 stopni.
Ten kąt jest sumą dwóch kątów: pomiędzy prostymi niebieską i zieloną oraz zieloną i żółtą. Łatwo zauważamy, że pierwszy z nich ma miarę równą kątowi B, a drugi miarę równą kątowi A.
Obeszło się elementarnie, bez trygonometrii. Co to w ogóle jest trygonometria? 😉
Mam przygotowany rysunek, ale nie umiem go wkleić. Spróbuję opisowo.
Na siatce kwadratowej rysujemy prostokątny trójkąt równoramienny, którego przyprostokątne są przekątnymi prostokątów o bokach 1 i 2 długości boku kwadratu siatki oznaczanej dalej przez A. Przeciwprostokątna jest przekątną prostokąta o bokach 1A i 3A. W każdym wierzchołku kąta ostrego narysowanego trójkąta mamy poglądowe rozwiązanie zadania: kąt trójkąta jest połową kąta prostego (z własności trójkąta prostokątnego i równoramiennego). Reszta z kąta prostego kwadratu siatki w tym wierzchołku to właśnie suma szukanych kątów.
Może chodzić np. o wzór na sumę tangensów: tga+tgb = sin(a+b)/(cosa*cosb), który można łatwo wyprowadzić korzystając z definicji tangensa i wzoru na sinus sumy. U nas tg a=1/3, tg b = 1/2, stąd suma jest 5/6. Kosinusy są odpowiednio 3/sqrt(10) i 2/sqrt(5). Jak się podstawi do wzoru, okaże się, że sin(a+b) = 1/sqrt(2), czyli a+b = 45 stopni.
http://postimg.org/image/quqhk81j9/
Czerwone linie są ewidentnie prostopadłe, a z symetrii widać, że zielona jest dwusieczną kąta między nimi.
Narysujmy trzy identyczne kwadraty bezpośrednio poniżej rysunku, tworząc siatkę kwadratów 3*2. Oznaczmy węzły siatki, poczynając od góry: (wiersz górny:) A,B,C,D; (wiersz środkowy:) E,F,G,H; (wiersz dolny:) I,J,K,L. Przekątna EK wyznacza kąt KEH równy danemu kątowi CEH=kąt(b). Łącząc punkty D i K otrzymuję trójkąt równoramienny prostokątny DEK (DK=KE=SQR(5), ED=SQR(10)), w którym kąt DEK=kąt EDK=PI/4. Kąt DEK=kąt(a)+kąt(b)=PI/4=kąt(c).
cbdo.
komentarze uwolnione, znaczy… błędne?
BTW problem podobny do tego z Drabiną Jakubową
Komentarze nie są błędne tylko są dowodami (rozwiązaniami) trygonometrycznymi, a chodzi o dowód geometryczny.
mp
(i+2)(i+3) = 5 + 5i, czyli a+b=c
a tera gełometria.
Z lewego dolnego narożnika w prawo i do góry pod kątem 45 stopni względem podstawy rysujemy odcinek o długości 2 przekątnych kwadratu.
Potem zakręcamy o 90 stopni i rysujemy w prawo i dól odcinek
o długości 1 przekątnej, dochodząc do prawego górnego rogu prostokąta. W ten sposób dorysowaliśmy trójkąt prostokątny o stosunku przyprostokątnych 2:1 oparty na przekątnej prostokąta widocznego na rysunku (o bokach 1 i 3). Kąt przy
lewym dolnym wierzchołku nowego trójkąta równa się b z podobieństwa trójkątów. Skoro bok dorysowanego trójkąta leży na przekątnej lewego kwadratu, to a + b = 45 stopni = c. c.b.d.o.
Dzień dobry, (jak zwykle) bardzo przyjemna łamigłówka. Oto rozwiązanie przy pomocy jednego rysunku na kartce w kratkę: https://www.desmos.com/calculator/08ub5f018b
http://s29.postimg.org/6c13vkirr/Untitled.png
Jak widać z rysunku: mamy tu trójkąt równoramienny z kątem 90st przy równych ramionach, co za tym idzie, dwa pozostałe kąty są równe i wynoszą:
(180-90)/2=45;
Z rysunku widać, że jeden z tych 45 stopniowych kątów to suma kątów ‚a’ i ‚b’.
c.n.d.
Umieszczam rysunek w układzie współrzędnych XOY.
Kwadrat o bokach równych długości przekątnej prostokąta 3×1 ma np wierzchołki: A(-2,0), B(1,1), C(0,4), D(-3,3).
Kwadrat o bokach równych długości przekątnej prostokąta 2×1 ma wierzchołki: B(1,1), F(2,3), C(0,4), E(-1,2).
Kąt BCO=a, kąt ACO=b, kat ACB=a+b=45 stopni (kąt między bokiem kwadratu, a jego przekątną)
Przecież mój dowód jest geometryczny, tylko że opisowy 🙂 Muszę jakoś wkleić rysunek?
Nie, jest OK, dlatego nie jest uwolniony.
mp
Trudno opisać dowód graficzny. Jeden obrazek jest tu lepszy niż 1000 słów:
https://docs.google.com/drawings/d/1AUcOrpQGzbYXSBjBqz5b7YTSxuNG4mfwhbbKJBt88Rk/edit?usp=sharing
Ale słowami ująłbym to tak:
Wyobraźmy sobie drugi szereg 3 kwadratów ułożony na tym pierwszym.
Z wierzchołka, w kórym jest kąt „a” poprowadźmy przekątną przez dwa kolejne kwadraty.
A na koniec jeszcze jedną przekątną w górnym prawym kwadracie w kierunku „Szczecin-Rzeszów”
Jak już to mamy narysowane, widzimy, że w dolnym lewym kwadracie mamy wierzchołek podzielony na 3 kąty. Są to a, b i c.
„a” to jest ten wyjściowy kąt z zadania.
„c” to jest 45 stopni przy przekątnej kwadratu, tak samo jak w prawym dolnym rogu.
A między nimi jest kąt „b”, bo ma taką samą proporcję przyprostokątnych jak ten z zadania.
Czyli a+b+c=90
A że c=45, to a+b= 45 = c
Wprowadźmy oznaczenia wierzchołków: A – z kątem a; B – z kątem B; C z kątem C; D – punkt wspólny żółtych (pomarańczowych? ugierowych?) linii, czyli prawy górny róg obrazka.
Ponadto niech sqrt(x) oznacza pierwiastek kwadratowy z liczby x.
Da się zauważyć, że trójkąty ACD i BCD są podobne – ich boki są w proporcji 1 : sqrt(2) : sqrt(5) (a współczynnik skalowania to sqrt(2)).
Zatem kąty w obu trójkątach to odpowiednio a, b i (Pi – c). Znając sumę kątów trójkąta możemy zapisać równanie:
a + b + Pi – c = Pi, skąd a + b = c.
Oznaczmy wierzchołki tak jak na rysunku. Natomiast długość boku każdego kwadratu niech będzie równa x.
Z równości trójkątów AEF oraz AED mamy oczywisty wniosek, że kąt AEF=a
Dalej mamy:
AE=x*sqrt(10)
BE=x*sqrt(5)
CE=x*sqrt(2)
Zatem kolejne ilorazy:
AE/BE=sqrt(2)
AC/CE=sqrt(2)
CE/BC=sqrt(2)
Dochodzimy teraz do sedna całej łamigłówki.
Otóż z równości powyższych ilorazów jasno wynika, że mamy do czynienia z podobieństwem trójkątów AEC oraz EBC a kąt AEC=b
Oczywistym jest, że kąt FEC=c
Kąt FEC jest oczywiście sumą kątów AEF oraz AEC
Więc c=a+b
O to chodziło?
jeszcze rysunek z oznaczeniami
http://bankfotek.pl/view/1822328
A ja oczywiście zrozumiałem, że chodzi o dowód trygonometryczny 🙂
W tego typu zadaniach zazwyczaj trzeba sprytnie coś dorysować, i wszystko staje się jasne. W tym wypadku skupiłem się na kwadracie środkowym z rysunku, tym z zaznaczonym kątem b. Niech wierzchołek tego kąta nazywa się B, a bok pionowy niech przecina ramię kąta a w punkcie A, oczywiście długość odcinka AB jest równa 1/3 boku kwadratu. Teraz łączymy punkt A z prawym dolnym wierzchołkiem środkowego kwadratu, niech to będzie C, czyli jakby odbijamy symetrycznie ramię kąta a względem prostej AB. Ten odcinek przecina ramię kąta b w punkcie P. Jeśli w punkcie P umieścimy początek układu współrzędnych, to przesuwając się zeń o wektor (2,1) znajdziemy się na ramieniu kąta b, a przesuwając o wektor (3,-1) – na tym „odbitym” ramieniu kąta a, czyli PC. Łącząc te punkty, dostajemy trzeci bok trójkąta, odpowiedni wektor ma współrzędne (1,-2), tak więc jest prostopadły do (2,1) i oczywiście tak samo długi, a więc mamy trójkąt równoramienny prostokątny, w którym poszukiwany kąt przy wierzchołku P ma 45°, a on jest równy sumie kątów a i b, o którą chodzi. Łatwiej niż czytać o tych wektorach, narysować to sobie, zwłaszcza na kartce w kratkę 🙂 albo na szachownicy łączymy pola a2 z c3 i a2 z d1, a następnie c3 z d1. Jak kogoś nużą te oznaczenia, niech skupi się tylko na szachownicy, od razu widać.
Można też inaczej, np. poprowadźmy wysokość z P na bok BC do punktu S: łatwo zauważyć, że punkt S dzieli odcinek BC w stosunku 2:3, czyli jeśli BC jest równe np. 10, to BS = 4, SC = 6 (a SP = 2). Tym samym możemy obliczyć wszystkie boki trójkąta rozwartokątnego BPC, korzystając z twierdzenia Pitagorasa. Trójkąt jest rozwiązany i na parę sposobów (najszybciej chyba z porównania wzorów na pole, bo wysokość jest znana) można obliczyć kąt rozwarty BPC, który wychodzi 135°, a więc suma kątów a i b jest 45°, c.n.d.
No ale znów może być zastrzeżenie, bo jednak pod koniec wchodzi trygonometria, jako że poznajemy kąt po jego sinusie, czy cosinusie 🙂
To jest chyba najprostszy dowód graficzny ???
http://pokazywarka.pl/kagfd8/
Tak, to jest TO!
mp
Looking on the most right of the three squares:
The two lines divide the left side of the rightmost square in three sections. The one at the bottom represents angle B, the one at the top represents angle A (top triangle in the rightmost square is identical with the bottom triangle of the leftmost square), and the middle section represents the difference between angle C and the sum of angles A and B.
Taki artykuł znalazłem: http://www.deltami.edu.pl/temat/matematyka/gry_zagadki_paradoksy/2014/11/28/Polszczyzna_z_wloszczyzna/ 🙂
Ja mam w streszczeniu dokładnie to co Spytko, i inni, tylko zamiast jednego rysunku, użyłem tysiąca słów 🙂