Wieżoskoczki
W komentarzu do wpisu Nieregularnie nie konno Esteon zadał tzw. dobre pytanie: „ile jest kombinacji ustawienia 8(9?) wieżoskoczków na szachownicy? (pewnie o tym już było, ale nie pamiętam)”.
Pytanie jest dobre, bo ja również nie pamiętam, aby odpowiedź pojawiła się w Łamiblogu; mało tego – nie pamiętam, aby pojawiła się gdziekolwiek (jeśli dobrze rozumiem pytanie).
Pierwszy raz stykam się z określeniem „wieżoskoczek” (całkiem przyjemne). Rozumiem, że chodzi o figurę, którą można wykonywać takie ruchy, jak wieżą i skoczkiem, czyli sytuacja podobna, jak w przypadku hetmana, łączącego w sobie ruchy wieży i gońca. W problemistyce szachowej taka figura zwana jest cesarzową, natomiast w grach (odmiany szachów) – najczęściej kanclerzem. Rozumiem też, że w pytaniu chodzi o liczbę różnych ustawień największej liczby wieżoskoczków na szachownicy (8×8) w taki sposób, aby żadne dwa wzajemnie się nie atakowały.
Od dawna znane są odpowiedzi na analogiczne pytania dotyczące wież i skoczków, natomiast ustawienia wieżoskoczków analizował w latach 30. XX w. znany brytyjski problemista Thomas Dawson, ale niezbyt skutecznie – ograniczył się do małych plansz. Jego zmagań, o ile wiem, nikt dotąd nie kontynuował. Czyżby problem był tak trudny obliczeniowo, czy może tak mało interesujący?
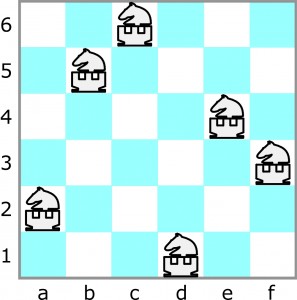
6 wieżoskoczków stoi na szachownicy 6×6 bezpiecznie, czyli nie atakując się nawzajem.
Proszę wykonać trzy ruchy trzema wieżoskoczkami – w tym przynajmniej jeden konikowy – tak, aby powstało inne bezpieczne ustawienie.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.

Komentarze
Trzy ruchy trzema wieżoskoczkami, czyli trzy ruchy każdym spośród trzech wybranych wieżoskoczków czy każdym z wybranych wieżoskoczków jeden ruch?
Trzy ruchy w sumie, czyli jednym cyk, drugi myk i trzecim pyk 🙂
mp
W pewnym sensie nie widzę różnicy między cesarzową (wieżoskoczkiem), a hetmanem (wieżogońcem), więc problem obliczeniowy i atrakcyjność zagadnienia powinny być podobne.
1) (WS)ac2
2) (WS)bb6
3) (WS)a5
prościzna 🙂
d1 —> b2
a2 —> a1
b5 —> d5
Tyż prowda (dlaczego „tyż”?).
mp
a można też tak:
b5 —> b6
c6 —> a5
a2 —> c2
Zastanawiam się czy zadanie ma jedno rozwiązanie. Nie jest zbyt skomplikowane, więc jeżeli będę dysponował wolnym czasem, zastanowię się nad tym.
Tymczasem podaję rozwiązanie, które mnie nie zadowala:
1. c6-a5 (ruch skoczka),
2. b5-b6,
3. a2-c2.
Rozwiązanie mnie nie zadowala, gdyż można je osiągnąć bez ruchu skoczka, dlatego podejrzewam, że nie jest jedyne.
Istotnie, to nie jedyne rozwiązanie, ale drugie również nie jest „zadowalające”.
Ciekawy jest jednak problem, czy w ogóle jest możliwe przekształcenie A->B (A i B to bezpieczne ustawienia 6 wieżoskoczków na planszy 6×6 – wszystkich takich różnych ustawień jest 21) trzema ruchami trzech wieżoskoczków w taki sposób aby:
– jeden ruch w A->B był konikowy
– A->B nie było możliwe bez ruchu konikowego.
Wydaje się, że nie, bo po ruchu konikowym pojawiają się dwa puste rzędy, które trzeba zapełnić dwoma wieżowymi ruchami wieżoskoczków stojących w rzędach, w których są dwie figury. Inaczej mówiąc, wszystkie trzy ruszane figury mają także wieżowy dostęp do pól, na których pojawiają się w ustawieniu B.
mp
1)
d1-b2
a2-a1
b5-d5
2)
c6-a5
b5-b6
a2-c2
Jeszcze można zrobić tak:
1. b5-d5,
2. d1-b2 (skoczek),
3. a2-a1.
Pozdrawiam.
Można zadanie zmodyfikować w taki sposób: proszę wykonać jeden ruch konikowy każdym wieżoskoczkiem – tak, aby powstało inne bezpieczne ustawienie. Ale to chyba jest za proste na łamigłówkę 😉
Moim zdaniem fajne i nie prostsze niż to we wpisie. Szkoda tylko, że rozwiązania są trzy (ściślej: możliwe są 3 różne końcowe ustawienia).
mp
a2 na c2, b5 na b6, c6 na a5.
Sa dwa rozwiazania:
1. Sa5-Wb6-Wc2
2. Sb2-Wd5-Wa1
a
Hurra. To już moje drugie dobre pytanie na tym blogu.
Wpiszę sobie do CV.
Trzy ruchy
1. b5 d5
2. d1 b2
3. a2 a1
Można to zrobić na wiele sposobów w 2 ruchach, np:
c6 c4
e4 e6
W trzech ruchach bez ruchu skoczkiem
e4 e6
c6 c2
a2 a4
Czy ktoś już policzył ile jest różnych ustawień wieżoskoczków na planszy 8×8?
Mi nadal nic na ten temat nie wiadomo.
mp
8 wieżoskoczków możemy na planszy 8×8 ustawić, tak by się wzajemnie nie atakowały, na 2766 sposobów.
Odpowiedzi szukałem wśród 8! rozwiązań problemu dla wież. W układzie współrzędnych położeniu wież odpowiada położenie odpowiednich punktów – od (1,1) do (8,8). Wśród 8! „rozdań” 8 punktów-wież wystarczy wybrać te warianty, wśród których nie znajdujemy żadnej pary punktów, której kwadrat odległości wynosi 5.
W arkuszu kalkulacyjnym rachunki wcale niestraszne (choć wyjściowy plik ma… 36Mb).
Wbrew pozorom, nie o to chodziło. Dlaczego? – wyjaśnię w następnym wpisie, choć zapewne nietrudno się domyślić.
mp