Trudna siódemka
Zadania, które zaproponowano łamigłówkowym sprinterom w pierwszych mistrzostwach świata (Nowy Jork, 1992) były spacerkiem w porównaniu z tym, z czym zmagają się oni w ostatnich latach. Zdolny uczeń szkoły podstawowej, który dziś zmierzyłby się z łamigłówkami sprzed 18 lat, uporałby się z niemal każdą w parę minut. Wówczas organizatorom po prostu zależało, aby to, co rozwiązują najlepsi, nadawało się także do zaoferowania przeciętnemu miłośnikowi intelektualnej rozrywki. Ważniejszy był cel ogólny, czyli popularyzacja mądrej formy relaksu, niż organizowanie niszowej imprezy dla bzików.
Niedawno rozwiązywałem część zadań przygotowanych na 19. mistrzostwa świata i przy wielu zwyczajnie odpadałem. Nie dlatego, żebym w ogóle nie dawał rady, tylko że przekraczałem „granicę bólu” – i to nie będąc pod presją. Byłoby nietaktem i przesadą stwierdzenie, że w związku z tym współczuję startującym w mistrzostwach, zatem napiszę, że ich podziwiam.
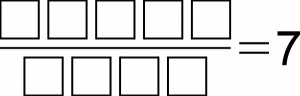
Wracając do Nowego Jorku, oczywiście, nie wszystko było takie łatwe, trafiło się kilka nieco twardszych orzeszków. Jeden z nich był dziełem znanego japońskiego speca od łamigłówek Noba Yoshigahary. Pamiętam, że autor niespokojnie chodził po sali, na której trwały zawody i dyskretnie zaglądał uczestnikom „w papiery”. Zwierzył mi się, że jest nieco zakłopotany, ponieważ nie zauważył, aby ktokolwiek rozwiązywał jego zadanie. Przyjrzałem się temu dziełku – w pierwszej chwili skojarzyło mi się z tzw. działaniami pandigitalnymi, które są raczej ciekawostkami lub łamigłówkami dla komputerów. Było najbliższe znanemu skądinąd zaszyfrowanemu dzieleniu:
W kratki należy wpisać różne cyfry od 1 do 9 tak, aby działanie było poprawne. Rozwiązywanie tego twardziela „na piechotę” to raczej pokuta, niż rozrywka, chyba że ktoś lubi pokutować. W dodatku rozwiązań jest pięć.
W zadaniu Noba jeden ułamek był zastąpiony sumą dwóch:
Pozostałe reguły nie zmieniły się.
Czy istotnie uporanie się z tą łamigłówką bez komputera jest trudne? I jak duży jest udział metody prób i błędów w dochodzeniu do rozwiązania?
Zacząć łatwo, lokując „na logikę” jedynkę w jedynej kratce, do której pasuje. Ale co dalej?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.
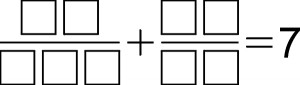

Komentarze
95/247+86/13=7
Przyznam, ze bylo troche metod prob i bledow, ale jakos tak intuicyjnie prawie od razu poszlam dobra sciezka.
Zadanie b. pomyslowe i niezbyt trudne. Rozwiazuje sie krok po kroku na logike przy bardzo malym udziale metody prob i bledow
95/247 + 86/13
a
95/247+86/13=7
Mam jedno z rozwiązań pierwszej łamigłówki: 16758:2394=7.
Pozdrawiam 🙂
Rozwiązanie drugiej łamigłówki to: 95/247 + 86/13 = 7.
Pozdrawiam 🙂
> Czy istotnie uporanie się z tą łamigłówką
> bez komputera jest trudne?
Dla mnie byłoby trudne z komputerem 🙂 Nie umiem programować.
> I jak duży jest udział metody prób
> i błędów w dochodzeniu do rozwiązania?
Ja nie robiłam tego metodą prób i błędów (chyba), tylko metodycznie sprawdzałam liczba po liczbie… Na szczęście sprawdzania nie było dużo. O wiele więcej czasu zajęło mi wymyślenie, jakie liczby sprawdzać.
> Zacząć łatwo, lokując „na logikę” jedynkę
> w jedynej kratce, do której pasuje. Ale co dalej?
To miejsce to mianownik drugiego ułamka, tam będzie jakieś naście. Dalej to trzeba było wpaść na to, że cały drugi ułamek ma wynosić „prawie 7”. I zacząć podstawianie: jeśli w mianowniku jest 12, to w liczniku będzie „coś nieco mniejszego od 84”, czyli może 83, może 79, może 78, może 76 (szybko można się zorientować, kiedy branie mniejszych liczb przestaje mieć sens). Wtedy bierzemy na warsztat 13 w mianowniku i „coś nieco mniejszego od 91” w liczniku, czyli 89, 87, 86… I właśnie 86 to jest nasze bingo 🙂