Jak to się robi…
Nikt nie poradził sobie z siatkarskim zadaniem z poprzedniego wpisu, a przynajmniej nie pochwalił się w komentarzu. Co prawda proste nie było, ale nie przypuszczałem, że aż tak. Jestem zaskoczony, bo liczba odwiedzających Łamiblog jest, mówiąc oględnie, niemała, choć komentatorów – jak to zwykle bywa – znacznie skromniejsza. Być może pogoda nie sprzyja główkowaniu, a może wszyscy, zwłaszcza maturzyści, kują do egzaminów. Jakkolwiek by nie było, postanowiłem – jak mówi znajomy nauczyciel – „odwalić kawałek dobrej (mam nadzieję), nikomu niepotrzebnej (mam nadzieję, że nie) roboty edukacyjnej”. Opiszę mianowicie, w ramach podpowiedzi, jak radziłbym sobie z prostszym o jeden szczebel wariantem tej łamigłówki. Zacznę od przypomnienia zadania w ogólnej formie.
W turnieju siatkówki startowało n drużyn. Każda rozegrała jeden mecz z każdą z pozostałych. Dla każdych m drużyn (oczywiście m < n) można wśród pozostałych wskazać taką, która pokonała każdą z tych m. Proszę znaleźć najmniejsze możliwe n.
Dla m = 1 przypadek jest trywialny. Każda drużyna przegrywa i wygrywa jeden mecz, czyli w turnieju uczestniczą trzy.
Dla m = 2 zadanie się komplikuje i to od razu dość mocno.
Każda drużyna uległa x zespołom i pokonała y. Rozważmy sytuację drużyny A pokonanej przez należący do x zespół B, czyli:
B powinna przegrać przynajmniej z jedną z pozostałych x, bo inaczej para A–B nie miałaby swojego pogromcy. Uogólniając, każda z drużyn x musiała doznać przynajmniej jednej porażki z inną drużyną z x, a stąd wniosek, że x jest nie mniejsze niż 3 (tu kłania się wariant dla m = 1).
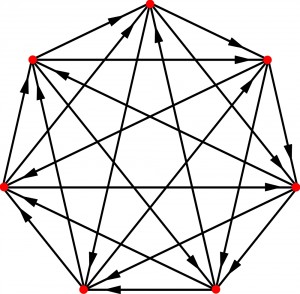
Z drugiej strony wśród wszystkich zespołów musi być choć jedna taka drużyna A, która wygrała co najmniej tyle meczów, co przegrała (w przeciwnym wypadku ogólna liczna zwycięstw byłaby mniejsza od ogólnej liczby porażek). Ta drużyna dozna przynajmniej trzech porażek z zespołami z x oraz pokona nie mniej niż trzy drużyny z y, a to możliwe jest tylko wówczas, gdy wszystkich drużyn będzie co najmniej 7. Proste?
Dowodem, że to możliwe, jest poniższy graf turnieju z udziałem 7 drużyn. Każda para wierzchołków jest „osaczona” przez dwie strzałki-porażki wychodzące z trzeciego wierzchołka.
A teraz proszę spróbować samemu uporać się z wariantem dla m = 3.
