Najmniej drużyn

23 kwietnia 2009
Marek Penszko

Dziękuję Jazzowi, pixlowi i Michałowi, także w imieniu mojego niepołamanego ołówka, za eleganckie dowody, że:

nie ma takich pięciu liczb naturalnych (bez zera) niepodzielnych przez 3 i 7, by suma każdych dwóch z nich była podzielna przez 3 lub 7.

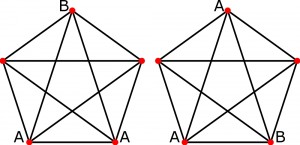
Na wyróżnienie zasługuje moim zdaniem dowód pixla – oparty na grafie i niemal klasyczny, bo bliski twierdzeniu i liczbom Ramseya. Pixl wykazał, że żaden graf pełny K5 (5 wierzchołków) bez klik monochromatycznych K3 nie spełnia warunków zadania („klika” to matematyczne określenie podgrafu pełnego, a więc stanowiącego część większego grafu pełnego).

Dowód można by uprościć, nie kolorując krawędzi, a pozostając tylko przy liczbach lokowanych w wierzchołkach. Powinny one należeć do dwu różnych podzbiorów – A i B (od tego zaczęli Jazz i Michał), przy czym w wierzchołkach żadnego trójkąta-kliki nie mogą występować liczby z tego samego podzbioru. Są zatem tylko dwa podstawowe sposoby umieszczenia liczb z podzbiorów A i B w wierzchołkach jakiegoś trójkąta, powiedzmy ostrokątnego:

W obu przypadkach nie da się oznaczyć dwóch pozostałych wierzchołków literami A i B tak, by nie pojawił się trójkąt „monoliterowy”, czyli dochodzimy do sprzeczności.

Korzystanie z grafów często bywa pomocne przy dowodzeniu, ilustrowaniu lub rozwiązywaniu zadań, w których występują zależności między podzbiorami, zwłaszcza gdy sformułowanie tych zależności powoduje lekki mętlik w głowie – jak w pamiętnej łamigłówce o dyngusowym polewaniu (dotychczas w komentarzach pod wpisem „Dziewki i parobcy” nie pojawiło się poprawne rozwiązanie; pomijając 1 parobka i 6 dziewek).

Oto inny przykład, łatwiejszy od „folwarcznego” zadania.

Zakończył się turniej siatkówki, w którym każde dwie drużyny rozegrały dokładnie jeden mecz.

Czyli na razie sprawa jest jasna, nic trudnego do zrozumienia – typowy system rozgrywek „każdy z każdym”, zwany także kołowym. I oto pojawia się stwierdzenie wprowadzające niejaki zamęt:

Dla dowolnych trzech drużyn można wskazać taką, która pokonała każdą z tych trzech.

I pytanie:

Ile drużyn startowało w turnieju, jeżeli liczba ta była najmniejszą, przy której mogło pojawić się to zadanie?