Dwa ciągi
Na 20. Łamigłówkowych Mistrzostwach Świata, zorganizowanych w roku 2011 w Budapeszcie, pojawiła się łamigłówka, której żywot był wyjątkowo krótki . Być może dlatego, że jej reguły oferują zbyt skromny repertuar konkretnych zadań, a może ze względu na dość żmudny proces rozwiązywania. Jednak z drugiej strony wydaje się całkiem pomysłowa i oryginalna, więc choćby z tego powodu zasługuje na przypomnienie.
Do rzędu k kratek należy wpisać cyfry od 1 do k/2 – każdą dwukrotnie – rozmieszczone tak, aby:
– dwie takie same cyfry nie sąsiadowały ze sobą;
– kolejne liczby jedno-, dwu- i trzycyfrowe – każda utworzona z kolejnych cyfr znajdujących się pod kolorową kreską – stanowiły ciąg rosnący. I podobnie ciąg rosnący powinny stanowić liczby utworzone z cyfr nad kolorowymi kreskami.
W poniższym przykładzie k=8, więc wpisywane są cyfry od 1 do 4, a w rozwiązaniu powstają dwa rosnące ciągi liczb: pod kreskami – 2<13<14<243 i nad kreskami – 21<31<42<43.
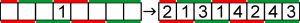
Uczestnicy wspomnianych Mistrzostw zmagali się z trzema takimi zadaniami. Tylko nieliczni poradzili sobie (w ograniczonym czasie) z najtrudniejszym – zamieszczonym poniżej (zakres wpisywanych cyfr – od 1 do 9).

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
123435456768789192
1<2<3<43<54<56<76<87<89<192
12<34<35<45<67<68<78<91<92
123435456768789192
Rozwiązaniem jest ciąg: 123435456768789192.
Cudne zadanie, z chęcią poznałabym pozostałe dwa zadania z Mistrzostw.
Będą w wakacyjnym „Omnibusie” (jeśli się ukaże)
mp
1<2<3<43<54<56<76<87<89<192
123435456768789192
12<34<35<45<67<68<78<91<92
Ciągle się zastanawiam, na czym polega trudność – a zadanie jest trudne. Dochodzę do wniosku, że nałożenie dwóch ciągów w taki sposób, że drugi wyraz pierwszego jest pierwszym drugiego i odwrotnie wywołuje serię mimowolnych pomyłek przypisania liczb do niewłaściwych ciągów.
Jedyne rozwiązanie to:
[1, 2, 3, 4, 3, 5, 4, 5, 6, 7, 6, 8, 7, 8, 9, 1, 9, 2]