Sześć zer
Łamigłówki „Trzy po trzy” to klasyka, choć dokładnie nie wiadomo, kiedy debiutowały. Prawdopodobnie przed około 100 laty w Anglii pod nazwą „Cross Math”, równocześnie z krzyżówkami liczbowymi. W Łamiblogu gościły dwukrotnie z okazji przełomu lat, bo do „uświetniania” takich okazji idealnie się nadają. Potwierdzeniem tego mogło być skorzystanie z analogicznej okazji przed czterema miesiącami, bo wówczas mogło się pojawić w Łamiblogu poniższe „3 po 3”.
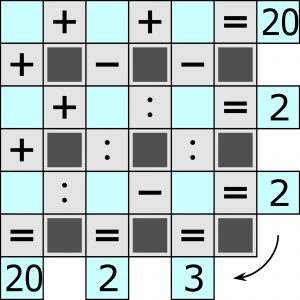
Przypomnę, że chodzi o wpisanie w puste kratki dziewięciu różnych cyfr – od 1 do 9 – tak, aby równości w trzech wierszach i trzech kolumnach były poprawne. Wyjątkowo obowiązuje zasada wykonywania działań po kolei – w wierszach od lewej do prawej, w kolumnach z góry na dół – czyli bez uwzględniania pierwszeństwa mnożenia i dzielenia.
Takie „3 po 3” jak wyżej jest o tyle ambitne autorsko, że wyniki działań nie są przypadkowe, tylko stanowią następstwo jakiegoś założenia lub przyjętej zasady. W tym przypadku są to kolejne „kawałki” liczb określających dwa sąsiednie lata. Inna moja ulubiona reguła jest skrajnie prosta: wszystkie wyniki powinny być taką samą liczbą. Kilka takich zadań z sześcioma jedynkami, dwójkami czy trójkami po znakach równości gościło w „Omnibusach”. A czy możliwe jest ułożenie takiego zadania z sześcioma zerami jako wynikami. Próbowałem, ale dotąd bezskutecznie. Nie udało mi się jednak udowodnić, że jest to niemożliwe. Mój najlepszy wynik to pięć zer i jakaś inna cyfra (jaka?) w poniższym zadaniu. Poza jego rozwiązaniem aktualne pozostaje więc pytanie o konstrukcję „3 po 3” z sześcioma zerami.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Zad.1
5 8 7
6 2 4
9 3 1
Zad.2
3 2 6
8 7 1
5 9 4
I drugie rozwiązanie ; ? nie jest cyfrą.
2 3 6
9 5 4
7 8 1
Kolejno rzędami:
3 2 6
8 7 1
5 9 4
Brakująca cyfra to 2.
Sprawdziłem programem i wygląda na to, że nie istnieje układ cyfr 1-9 dający sześć zer.
Są dwa rozwiązania, ale cyfrę w wyniku ma tylko jedno.
236
954
781
? = 0,5
326
871
594
? = 2
Zgodnie z moją najlepszą wiedzą:
– pod znakiem zapytania kryje się 2
– nie da się utworzyć konstrukcji „3 po 3” z sześcioma zerami
Zadanie „3 po 3” z sześcioma zerami dałoby się zrobić pod warunkiem zastosowania jakiejś sztuczki. Np., stawiając dziewiątkę „na głowie”, możemy otrzymać takie rozwiązanie:
6(9) – 1 – 5 = 0
2 + 6 – 8 = 0
4 – 7 + 3 = 0
https://zapodaj.net/b48650adffdec.png.html
Słupki obrazują ilość (pionowa skala) możliwych równań dla poszczególnych wyników (skala pozioma).
Jak widać dla wyniku zero mamy zauważalnie mniej możliwości do wyboru.
Przekłada się to na znaczące trudności z ułożeniem zadania z sześcioma zerami.
3×2-6=0
8-7-1=0
5-9+4=0
2
? = 2
Nie ma możliwości, by otrzymać sześć zer. Gdyby chcieć używać jedynie znaków „+” i „- ”, suma liczb z plusami musiałaby być równa sumie liczb z minusami a to niemożliwe, bo suma wszystkich jest nieparzysta (45). Trzeba więc podeprzeć się mnożeniem i/lub dzieleniem a jedynymi trójkami wchodzącymi w rachubę są {2,3,6} i {2,4,8}. Suma pierwszej trójki to 11, więc dla pozostałych dwóch rzędów pozostaje 34 i można pokombinować, by otrzymać zera – tak właśnie dzieje się w wierszach zadania. W kolumnach w dalszym ciągu mamy 45 i drugą trójkę krzyżującą się w dwójce z pierwszą. Niestety suma tej trójki jest parzysta, zatem dla dwu pozostałych kolumn pozostaje wciąż nieparzysta suma pozostałych liczb – nie sposób więc dla trzech kolumn otrzymać trzy zera.
3 2 6
8 7 1
5 9 4
Pod znakiem zapytania ukrywa się 2 = 6:1-4.
Zadanie 2022/2023:
Zadanie z zerami:
Brakującą cyfrą kryjącą się pod pytajnikiem jest:
zadanie 1.
587
624
931
zadanie 2.
326
871
594
?=2
Program mówi mi, że tego zadania z 6 zerami ułożyć się nie da 🙁
Ciekawostką jest to, że jeśli dopuścimy jedno niezero, obojętne gdzie, to wszystkie rozwiązania bazują na podziale zbioru {1,2,3,4,5,6,7,8,9}, w wierszach na podzbiory {1,7,8} {2,3,6} {4,5,9} i dualnym do niego w kolumnach na podzbiory {1,4,6} {3,5,8} {2,7,9}. Więc w pewnym, uogólnionym sensie, zadanie takie ma quasi jedno rozwiązanie.
Dzień dobry,
Część I:
5+8+7=20
6+2:4=2
9:3-1=2
i równania w pionie też się zgadzają wtedy.
Część II:
3×2-6=0
8-7-1=0
5-9+4=0
w pionie pierwsze dwa równania „schodzą” się do 0, trzecie równanie daje 2.
Część III:
nie umiem 🙁
Pozdrawiam, SG