Problem 49
W moim łamigłówkowym światku pojawiają się czasem – zwykle przypadkowo przy okazji innego tematu – problemy, a właściwie problemiki lub pytania, które trudno nazwać łamigłówkami, ale które chodzą po głowie i trudno się od nich uwolnić. Oto przykład takiego drobiazgu: czy 49 jest jedynym kwadratem, który pozostaje kwadratem zarówno po usunięciu pierwszej cyfry, jak i po usunięciu ostatniej? W encyklopedii OEIS jest ciąg kwadratów, które nie tracą kwadratowości po równoczesnym usunięciu cyfr pierwszej i ostatniej (A077355, przykłady – 196, 8649, 77841) – ale to oczywiście, wbrew pozorom, coś prawie całkiem innego. Wprawdzie w różnych numberopediach pojawia się liczba 49 ze względu na jej osobliwe własności, ale inne – na przykład jako najmniejsza konkatenacja (zlepek) dwóch kwadratów albo największy kwadrat liczby pierwszej p, który jest większy od iloczynu wszystkich liczb pierwszych mniejszych od p (49 > 2*3*5=30). To, że nigdzie nie ma wzmianki o podwójnie „obciachowej” jedynaczce 49 mogłoby sugerować, że nie jest ona jedynaczką. Można jednak dość łatwo dowieść, że jednak jest. W jaki sposób?
A przy okazji inne, bardziej „normalne” zadanie na temat.
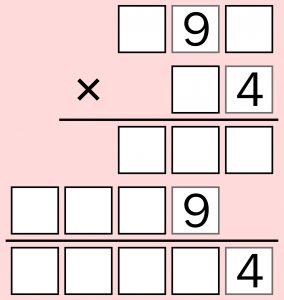
Zapisałem 49 kolejnych liczb naturalnych – od 1 do 49. Wykreśliłem dwie z nich, a zamiast nich do zbioru dopisałem ich różnicę (nieujemną, czyli moduł różnicy). Taką operację powtórzyłem 48 razy, aż pozostała jedna liczba. Jaka, jeśli liczbę tę można utworzyć z dwóch różnych cyfr spośród czterech, nie występujących w poniższym zapisie mnożenia – oczywiście po jego rozszyfrowaniu? W zapisie ujawniono czwórki i dziewiątki, ale niekoniecznie wszystkie.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Wyszło mi 23. Liczba możliwości, w jakie proces wykreślenia może przebiegać, mocno sugeruje, że należy się skupić na niezmiennych charakterystykach 🙂
OK
mp
Nie mam pomysłu, jak udowodnić, że 49 to jedynak, może jakaś drobna sugestia?
Końcówki kwadratów
mp
„Dość łatwa” część na razie nie taka łatwa, więc zadanie „normalne”. Wychodzi:
191×94 = 17954, iloczyny cząstkowe 764 i 1719. Nie ma cyfr 0, 2, 3, 8. Zaraz do nich wrócimy.
Suma liczb od 1 do 49 jest nieparzysta. Dwie liczby można wykreślić na 3 sposoby:
– parzystą i nieparzystą: różnica nieparzysta, zastępuje inną nieparzystą, jest tak, jakbyśmy wykreślili parzystą, czyli suma wszystkich dalej nieparzysta,
– dwie nieparzyste: różnica parzysta, suma tych dwóch nieparzystych była parzysta i zastępujemy ją parzystą, więc całkowita suma nadal nieparzysta,
– dwie parzyste: różnica parzysta, suma dwóch była parzysta, całkowita suma nadal nieparzysta.
Postępujemy tak dalej i zawsze zostaje suma nieparzysta, nie ma innej opcji. Jedyną liczbą nieparzystą, która da się ułożyć z cyfr 2, 3, 8, 0, i która może być różnicą liczb od 1 do 49, jest 23. Gdyby cyfry mogły się powtarzać, to dochodzi 33.
191×94=17954. Została liczba 23
23 lub 25, a także 35.
mnożenie to 191 * 94, cztery różne cyfry to 2,3,5 i 8. Wynik musi być liczbą nieparzystą <49 stąd zostają 3 opcje: 23, 25 i 35. sortujemy liczby od 1 do 48 i każdą parę redukujemy do 1 (2-1 itd), to daje nam 24 operacje i zbiór 24 jedynek i 49. Następnie 24 razy odejmujemy jedynkę od 49, otrzymując 25. Możemy też uzyskać dwie dwójki zmieniajac dwie kolejne pary liczb (np 4-2,3-1) i otrzymać 23.
Przy założeniu że różnica może wynosić 0 możemy też wyeliminować 10 jedynek i uzyskać 35.
Dowodu na jedynactwo 49 nie znalazłem.
A rozwiązaniem drugiego zadania jest chyba 23.
Mnożenie to 191 * 94 = 764 + 1719 = 17954. Do wyboru mamy zatem cyfry 0,2,3,8.
Możemy dopuścić 20, 23, 28, 32, 38 – dwucyfrowe mniejsze od 48.
Jedyna nieparzysta z nich to 23, a wydaje mi się, że nie można wskutek tych 48 operacji ułożyć liczby parzystej.
Dobry wieczór,
Wydaje mi się, że (ale nie mam pewności):
Mnożenie:
1 9 1
9 4
————————
7 6 4
1 7 1 9
———————–
1 7 9 5 4
Poszukiwaną liczbą jest 23 (generowana jako I para: 1 i 3, potem 2 i 4, potem 2 i 5, moduł różnicy i kolejna liczba,…….., 24, 48, potem 24, 49 i ostatnia para to 2 i 25; zostaje 23).
W temacie liczby 49 jako „jedynaczki” kilka zauważeń:
– gdy liczba kończy się dużą liczbą 0 to jest ona parzysta i wtedy skreślenie ostatniej cyfry powoduje, że liczba zer jest nieparzysta i dana liczba nie będzie kwadratem
– kwadraty liczb mają powtarzalne 2 cyfrowe końcówki co 50 liczb – kwadrat cyfry 1 ma taką samą „końcówkę” co kwadrat liczby 51, 101, 151 itd. 2 taką samą jak 52, 102, 152….
(zbiór 2-cyfrowych końcówek to: 1,4,9,16,25,36…..)
– jeżeli kwadratem jest liczba bez pierwszej cyfry to ma ona 3-cyfrową końcówkę (pomijam opisany przypadek 0 na końcu), 025, 625, 225; wtedy końcówki bez ostatniej cyfry to 02, 62 i 22 które nie należą to zbioru 2-cyfrowych końcówek)
Pozdrawiam, SG
Liczyłem na to, że ktoś podał dowod na samotność 49, ale widzę, że jednak nie! Czyżby dowód nie był taki łatwy jednak?
Po podpowiedzi o końcówkach kwadratów myślałem, że szybko rozgryzę, ale się nie udało.
Gospodarz chyba musi wspomóc:)
Gospodarz jest bezradny. Wie, że końcówki kwadratów są środkiem do celu (ale to nic odkrywczego), tylko nie wie jak tego środka użyć. Dowód rzeczywiście wygląda na twardy orzech, dotąd chyba nie rozgryziony. Gdyby tak było, to prawie na pewno w OEIS byłby namiar na ten dowód.
mp
Wielka szkoda, w takim razie porzucam swoje próby, najwyraźniej nie mój poziom 🙂
Po trudach poszukiwania dowodu przyda się…
Procedura relaksacyjna:
Poniższemu kwadratowi obcinamy kwadrat z lewej strony.
Następnie obcinamy mu kwadrat z prawej strony.
To co zostało (środkowa część) też powinno być kwadratem.
923521753424153664
Ciągu kwadratów, które są konkatenacją trzech kwadratów (jeszcze) nie ma w OEIS, ale jest ciąg konkatenacji dwóch (A039686).
m
Ciekawe dla ciekawych:
Konkatenacja trzech kwadratów, tworząca kwadrat pozostający kwadratem także po odczytaniu wspak.
Trzy składowe kwadraty po tym uwspaczeniu pozostają kwadratami gdyż są palindromami.
484484121