Ciężkie mebelki
Mebelki vel Heyawake należą do moich ulubionych rodzajów zadań, więc trudno mi się z nimi rozstać. Postanowiłem zatem uraczyć moich gości jeszcze jednym okazem w nadziei, że większość z Państwa podziela moje upodobanie. Wybrałem zaś przykład najtrudniejszy, jakim dysponuję. Czy podzielą Państwo moją opinię o stopniu trudności – to się okaże.
Przypominam w skrócie instrukcję obsługi, a gdyby pojawiły się jakieś wątpliwości, odsyłam do obszerniejszej instrukcji w poprzednim wpisie i zamieszczonego tam małego przykładu.
Czerwone linie dzielą diagram na prostokąty obejmujące kilka kratek. W większości prostokątów należy zaczernić niektóre kratki. Kolor prostokąta oznacza liczbę kratek, które trzeba w nim zaczernić: żółty – 2 czarne kratki, zielony – 1, niebieski – 0. Liczba kratek do zaczernienia w białym prostokącie nie jest podana, ale wynika jednoznacznie z zaczernień w sąsiednich prostokątach ze względu na dwa warunki:
1) zaczernione kratki nie mogą łączyć się bokami, a stykając się rogami nie mogą dzielić diagramu na części;
2) poziomy lub pionowy ciągły rząd niezaczernionych kratek nie może sięgać trzech prostokątów.
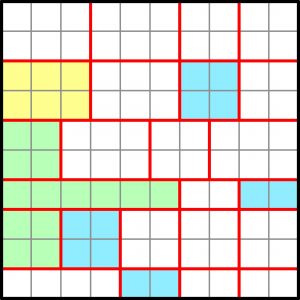
Jako rozwiązanie wystarczy podać, ile grup czarnych kratek występuje w rozwiązaniu. Grupę tworzą co najmniej dwie czarne kratki połączone rogami, a także jedna samotna kratka czarna owca, która jest tzw. grupą trywialną.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
13 grup
OOXOOOOXOO
XOOOXOXOOX
OOXOOXOOOO
OXOXOOOOXO
OOOOOXOXOO
XOXOXOXOOX
OOOXOOOXOO
OXOOOXOOXO
OOOOXOOXOO
XOXOOOXOOX
Chyba trzeba będzie się wziąć za te mebelki bo nic innego Pan Gospodarz nie wrzuca.
To będzie koniec meblowania. Na Wielkanoc szykuje się orzech diamentowej twardości.
mp
13
https://www.fotosik.pl/zdjecie/8a45fc8ba10a4ba0
9 trywialnych, po jednej 2-, 3, 4- i 11-elementowej, czyli w sumie 13. Dosyć trudna. Dla pewności zdjęcie:
https://www.fotosik.pl/zdjecie/8ec55e59b1a73535
13 grup ( 9 po jednej kratce, 1 -dwie kratki, 1- trzy kratki, 1- 4 kratki, 1- 11 kratek)
Faktycznie, jak dotąd najtrudniejsze, ale wciąż przyjemne w rozwiązywaniu 🙂
Ponownie 13 grup: 9 trywialnych, 2-elementowa, 3-elementowa, 4-elementowa i 11-elementowa.
Wyszło mi jak poprzednio 13. Przykład najtrudniejszy, ale poszedł mi chyba nawet szybciej niż poprzedni. Najtrudniejsze jest zliczenie grup 🙂