Biały kruk
Po brzozowym cichym lesie
Dziewczę idzie, dzbanek niesie,
Niesie dzbanek z jagodami,
Z jagodami borówkami.
Co wspólnego ma ten początek wiersza Teofila (nazwisko proszę) Jagoda z rokiem, który właśnie się zaczął? To bardzo trudna zagadka, więc spieszę z rozwiązaniem: łącznikiem jest termin „konkatenacja”, który ma kilka podobnych znaczeń. W literaturze jest powtórzeniem końcówki poprzedniego wersu na początku następnego (niesie; z jagodami), zaś w matematyce oznacza połączenie („sklejenie”) dwu liczb w jedną. Właściwie arytmetyczna konkatenacja to nic niezwykłego, bo jest nią każda liczba przynajmniej dwucyfrowa. Jednak 2021 to obiekt szczególny, bo połączenie dwu liczb kolejnych. Od poprzedniego i następnego takiego konkatenacyjnego roku dzieli nas 101 lat. Jeśli ponadto uwzględnić, że 2021 jest iloczynem dwu także kolejnych liczb pierwszych (43×47), to rok bieżący zasłuży na miano białego kruka. Następna liczba o takich dwu własnościach (konkatenacja dwu kolejnych liczb – najpierw mniejsza, potem większa – oraz iloczyn dwu kolejnych liczb pierwszych) wygląda tak:
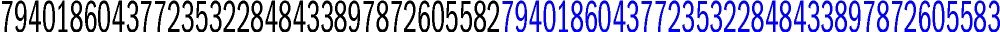
Iloczynem których dwu kolejnych liczb pierwszych jest ten 72-cyfrowy potwór – tego nie wiem, ale może komuś dysponującemu odpowiednim narzędziem do rozkładania takich gigantów uda się to ustalić.
Co jeszcze wyróżnia liczbę 2021? Chodzi oczywiście o cechy mniej trywialne a bardziej specyficzne niż np. to, że suma cyfr równa jest 5 albo brakuje czterech do kwadratu, ale też nie o cechy zbyt zawiłe (np. suma sum 24 par kolejnych początkowych liczb pierwszych, czyli (2+3)+(3+5)+(5+7)+…+(79+83)+(83+89)+(89+97)=2021).
Zapewne warto zauważyć, że:
– 2021 otrzymamy, zwiększając sumę 33 pierwszych liczb pierwszych o 33;
– odwrotka 2021, a więc 1202, także jest liczbą półpierwszą, czyli iloczynem dwu liczb pierwszych (2×601);
– suma 2021 i jej odwrotki jest palindromem (3223), co nie dziwi, natomiast osobliwość – właściwą tylko niektórym liczbom, nie zawierającym cyfr większych niż 2 – stanowi to, że iloczyn tych dwu liczb także jest palindromem (2429242);
– 2021 można zapisać jako sumę mniejszej liczby i sumy jej cyfr na dokładnie dwa sposoby: 1996+1+9+9+6=2021 oraz 2014+2+1+4=2021;
– ciąg Fibonacciego zawierający liczbę 2021 maksymalnie oddaloną od pierwszego wyrazu, zaczyna się liczbami (dodatnimi) 13 i 6: 13, 6, 19, 25, 44, 69, 113, 182, 295, 477, 772, 1249, 2021,…
– 2021 można zapisać jako sumę kolejnych liczb na 3 sposoby. Najprościej oczywiście jako 1010+1011. Jakie są dwa pozostałe sposoby?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
26 + 27 + 28 + … + 66 + 67 + 68 = 2021
(suma 43 liczb)
20 + 21 + 22 + … + 64 + 65 + 66 = 2021
(suma 47 liczb)
Dość łatwo znaleźć te sumy korzystając z faktu, że 2021 = 43*47.
Na wszelki wypadek sprawdziłem programem, że faktycznie nie ma innych przedstawień.
Faktycznie fakt, że 2021=43*47 jest mocną podpowiedzią.
mp
Rozwiązań jest 7, choć te zaczynające się od ujemnej liczby są analogiczne do tych dodatnich (w tym do tego, którego w zestawie nie ma, bo sumą nie jest).
2021 = a + … + b
a = -2020, b = 2021
a = -1009, b = 1011
a = -25, b = 68
a = -19, b = 66
a = 20, b = 66
a = 26, b = 68
a = 1010, b = 1011
47 składników: 20 + 21 +…….+ 66 = 2021
43 składniki: 26 + 27 + ……..+ 68 = 2021
Następna po 2021 taka liczba to 2307340946901148 2307340946901147
który jest iloczynem liczb pierwszych 4803478892324963 i 4803478892324969.
(jest tu połączenie odwrotne niż w przykładzie; liczba większa – liczba mniejsza)
26+…+68=2021
20+…+66=2021
2021 jest różnicą sum dwóch ciągów {od 1 do k} i {od 1 do n} (gdzie k<n)
n*(n+1)/2-k*(k+1)/2=2021
po przekształceniu
(n-k)*(n+k+1)=4042
4042=43*94
4042=47*86
(iloczyny 2*2021 i 1*4042 pomijam)
n-k=43 i n+k+1=94 (k=25 n=68)
n-k=47 i n+k+1=86 (k=19 n=66)
https://community.wolfram.com/groups/-/m/t/2148797
1.
2021 = Suma 47 wyrazów ciągu matematycznego (o kroku 1).
Środkowy wyraz ciągu to 43.
2.
2021 = Suma 43 wyrazów ciągu matematycznego (o kroku 1).
Środkowy wyraz ciągu to 47.
Jako ciekawostkę dorzucam ciągi Fibonacciego w których 2021 występuje na jak najdalszej pozycji.
[9, [2, 95, 97, 192, 289, 481, 770, 1251, 2021]]
[9, [23, 82, 105, 187, 292, 479, 771, 1250, 2021]]
[9, [44, 69, 113, 182, 295, 477, 772, 1249, 2021]]
[9, [65, 56, 121, 177, 298, 475, 773, 1248, 2021]]
[9, [86, 43, 129, 172, 301, 473, 774, 1247, 2021]]
[9, [107, 30, 137, 167, 304, 471, 775, 1246, 2021]]
[9, [128, 17, 145, 162, 307, 469, 776, 1245, 2021]]
[9, [149, 4, 153, 157, 310, 467, 777, 1244, 2021]]
[10, [25, 44, 69, 113, 182, 295, 477, 772, 1249, 2021]]
[10, [59, 23, 82, 105, 187, 292, 479, 771, 1250, 2021]]
[10, [93, 2, 95, 97, 192, 289, 481, 770, 1251, 2021]]
[11, [19, 25, 44, 69, 113, 182, 295, 477, 772, 1249, 2021]]
[12, [6, 19, 25, 44, 69, 113, 182, 295, 477, 772, 1249, 2021]]
[13, [13, 6, 19, 25, 44, 69, 113, 182, 295, 477, 772, 1249, 2021]]
Dla wcześniejszych pozycji wystąpienia liczby 2021 tych ciągów jest coraz więcej.
To jest histogram
[0, 0, 0, 1010, 337, 135, 51, 20, 8, 3, 1, 1, 1]
Na 4 pozycji 2021 pojawia się 1010 razy i.t.d…
Proszę wkleić Potwora 72 w postaci tekstowej.
20+21+…+66
26+27+…+68
Lenartowicz 🙂
Wszystkiego dobrego w Nowym Roku Panu i wszystkim także i ode mnie. Jeśli chodzi o zadanie, to można zauważyć, że przy nieparzystej liczbie składników od 1 do n ich suma będzie podzielna przez n, bo n jest podzielne przez n, (n-1)+1 jest podzielne przez n, itd, suma ta wynosi n*(n+1)/2. A dowolny inny n-wyrazowy ciąg, zaczynający się nie od 1 tylko od jakiegoś k, ma sumę wyrazów większą o (k-1)*n od tego bazowego zaczynającego się od 1, więc ta suma też jest podzielna przez n. Na przykład 1+2+3+4+5 = 15, dzieli się przez 5, a i taka suma jak np. 4+5+6+7+8 = 30 też dzieli się przez 5. Co więcej, każda liczba poczynając od 15 podzielna przez 5 da się przedstawić jako taka suma: 20 to 2+3+4+5+6, itd. Nasza suma dzieli się przez 43 i 47, a więc musi mieć raz 43 składniki, a raz 47. W pierwszym przypadku są to liczby od 26 do 68 (środkowy wyraz to 47) a w drugim od 20 do 66 (środkowy wyraz to 43).
Podpowiedzią jest fragment artykułu, w którym pada, że 2021 jest iloczynem liczb pierwszych (43×47)
20 + … + 66 = 2021 (47 składników sumy)
26 + … + 68 = 2021 (43 składniki sumy)
Korzystając z odpowiednich narzędzi można ustalić, że 72-cyfrowy potwór jest iloczynem bliźniaków:
a=891077215721081784886888257701070827,
b=891077215721081784886888257701070829.
Jeśli Teofil, to musi być Lenartowicz – tak mi zaświtało w głowie, a google potwierdził. Liczbę 2021 jako sumę kolejnych liczb można przedstawić tak:
20+21+…+65+66 (47 składników)
26+27+…+67+68 (43 składniki)
Znalezienie dwóch liczb pierwszych, których iloczynem jest 72-cyfrowy tasiemiec jest proste aczkolwiek pracochłonne. Trzeba policzyć pierwiastek kwadratowy z tasiemca, a następnie dzielić tę 72-cyfrową liczbę przez kolejne liczby nieparzyste większe od jej pierwiastka, z pominięciem kończących się cyfrą 5. Jeżeli iloraz wyjdzie całkowity, to wystarczy sprawdzić, czy dzielnik i iloraz są liczbami pierwszymi.
Dla 2021 pierwiastkiem jest 44,96 więc już pierwsze dzielenie to 2021/47.
Pierwiastek kwadratowy podanej 72-cyfrowej liczby zaczyna się tak: 8910… i ma (do przecinka) 36 cyfr. Po tyle samo cyfr mają szukane liczby pierwsze; jedna jest mniejsza od tego pierwiastka, a druga większa. Cyfry jedności tych liczb pierwszych to albo 1 i 3, albo 7 i 9. Po ustaleniu powyższych własności miałam zamiar przejrzeć listę 36-cyfrowych liczb pierwszych:
https://primes.utm.edu/curios/index.php?start=25&stop=36
i wyłuskać z niej właściwą parę sąsiednich liczb o żądanych początkach i końcach. Okazało się jednak, że nie ma tak łatwo. Strona nie zawiera bowiem kompletnej listy liczb pierwszych (cały czas jest uzupełniana). Interesująco wygląda podana tam liczba: 934361079326356530741942970523610389, ponieważ znajduje się w miarę blisko „8910…” oraz – jeśli akurat przypadkiem jest szukanym przeze mnie mnożnikiem – mnożna zaczynałaby się od „84979…”, czyli znajdowałaby z drugiej strony pierwiastka kwadratowego potwora, a tak miało być.
Jeżeli będziemy mocno trzymać kciuki, to może się okazać, że już pierwsze dzielenie, o którym pisze Michał S, ustali te dwie liczby.
Stanie się tak, jeśli są one bliźniacze.
794018604377235322848433897872605582794018604377235322848433897872605583
=
891077215721081784886888257701070827
*
891077215721081784886888257701070829
P.S.
Do obliczenia jest oczywiście konieczny pierwiastek z Potwora72. Zaskakujące, ale Wolfram tego nie potrafi! Przynajmniej w bezpłatnej wersji. Trzeba mieć odpowiedni program.
Potem już prosta sprawa, gdyż dla liczby 36-cyfrowej Wolfram umie sprawdzić, czy jest ona pierwsza. Dwa strzały i od razu celne, gdyż rzeczywiście są to liczby bliźniacze.
Problem byłby większy, gdyby Wolfram nie potrafił potwierdzić pierwszości… Oszacowałem, że używając sita Eratostenesa trwało by to ok. 10^20 lat (sto trylionów).
2021 = 20 + .. + 66,
2021 = 26 + .. + 68,
794018604377235322848433897872605582794018604377235322848433897872605583 = 891077215721081784886888257701070827 * 891077215721081784886888257701070829.
W poprzednim wpisie przedstawiłem dwa rozwiązania z nieparzystą liczbą składników (43 i 47), ale nurtowało mnie, jak w miarę prosto uzasadnić, że poza trywialnym 1010+1011 nie da się ułożyć sumy z parzystą liczbą składników.
Po pierwsze, jeśli liczba składników jest podzielna przez 4, to ich suma zawsze będzie parzysta, więc nigdy nie 2021.
Po drugie, liczba składników jest podzielna przez 2, ale nie przez 4, więc może być na przykład 6. Suma sześciu składników zawsze jednak będzie podzielna przez 3, a 2021 nie jest ani przez 3, ani przez 5 (co odpowiadałoby dziesięciu składnikom, bo dla 2n składników suma jest podzielna przez n), ani przez żadną liczbę nieparzystą mniejszą od 43, mniejszego z pary (43,47) dzielników 2021. Szansa pojawiłaby się więc dopiero przy liczbie składników, równej 86 – ale najmniejsza taka suma, liczb od 1 do 86, wynosi 3741, dokładnie 43*87. Zwiększając każdy ze składników o 1 otrzymamy sumę zwiększoną o 86, tak więc jeśli chcemy mieć podzielność przez 47, to następną okazję daje 47*3, czyli 141. Suma liczb od 28 do 113 daje 6063, co z łatwością identyfikujemy jako 2021*3. Ale ciekawe jest zezwolenie na liczby ujemne, idąc niejako w drugą stronę od 3741: suma liczb od -19 do 66 daje tyle ile trzeba, czyli 2021 (86 składników, suma pierwszego i ostatniego 47). A jak zamienimy miejscami 43 i 47, to dostaniemy 94 składniki, suma pierwszego i ostatniego 43, a więc od -25 do 68.
2021 = 20+21+…+66
2021 = 26+27+…+68
Czyli te fragmenty ciągu arytmetycznego o różnicy jeden, których środkowym wyrazem jest jeden z (właściwych) dzielników numeru roku, a długością drugi.
26 + 27 + 28 + … + 68 = 2021 (liczba składników sumy: 43)
20 + 21 + 22 + … + 66 = 2021 (liczba składnikow sumy: 47)
Pierwszy wyraz a ciągu jest powiązany z liczbą wyrazów p ciągu następująco:
a = 2021/p – (p-1)/2
p jest dzielnikiem liczby 2021 z przedziału liczb naturalnych (warunek wynika stad, ze a > 0; trzeba rozwiązać równanie kwadratowe ze względu na p i deltę). Dla p=1 wynikiem jest po prostu liczba 2021. Pozostałe dzielniki liczby 2021 to 43 i 47 (oraz 2021, ale 2021 leży poza przedziałem ).
Uzupełnienie: z mojego poprzedniego komentarza zniknął przedział dla p: .
Ponownie podaje przedział: ( 0 , 65 )