Konik polny

30 stycznia 2010
Marek Penszko

Mam słabość do szachów, a zwłaszcza do wariacji na ich temat, czyli zadań szachowych z fantazją. Wiedzą o tym stali bywalcy Łamiblogu, choć zapewne wielu z nich odpuszcza sobie wpisy dotyczące szachów zwanych bajkowymi, bo są jakby z innej parafii, więc nie każdemu podchodzą. Przypomnę, że w szachach bajkowych pojawiają się na przykład różne dziwne figury – jako uzupełnienie tradycyjnych i zwykle z tradycyjnymi spokrewnione. Pisałem już szerzej o kilku z nich, o niektórych całkiem niedawno (cesarzowa), ale o najważniejszej – koniku polnym – tylko pobieżnie przed ponad dwoma laty. Może więc warto, aby pohasał swobodniej i w roli głównej na większym wybiegu.

Konika polnego wymyślił Thomas Rayner Dawson w roku 1912 jako jedną z pierwszych figur bajkowych. Była ona także pierwszą oficjalnie zaakceptowaną przez Międzynarodową Federację Szachową (FIDE), a ściślej przez jej organ zajmujący się problemistyką. Można powiedzieć, że konik polny przetarł drogę do FIDE innym figurom bajkowym, zwanym oficjalniej i dostojniej heterodoksyjnymi. Dziś pod skrzydłami Federacji występuje ich kilkanaście, chociaż nie wszędzie mają wstęp. Pojawiają się w konkursach i mistrzostwach polegających na układaniu zadań, ale nie akceptują ich solverzy (solving to sport umysłowy dla szachowych „szybkorozwiązywaczy”). To trochę tak, jakby w mistrzostwach sudoku rozwiązywać wyłącznie klasyczne zadania.

Konik polny (Kp) porusza się wzdłuż tych samych linii co hetman, ale ruch nim polega na przeskoczeniu przez najbliższą bierkę (dowolnego koloru) i stanięciu na polu bezpośrednio za nią. Jeżeli na tym polu stoi bierka przeciwnika – zostaje zbita, jeżeli własna – ruchu nie można wykonać. Inaczej mówiąc, Kp atakuje i może osiągnąć w danym ruchu tylko pole tuż za najbliższą bierką, stojącą w tym samym rzędzie, kolumnie lub na przekątnej. Jak z tego wynika, figura ta jest bez innych bierek bezradna – unieruchomiona, a bez wsparcia własnych nic nie zwojuje i właściwie pozostaje bezbronna. W sprzyjających okolicznościach może jednak okazać się całkiem niebezpieczna.
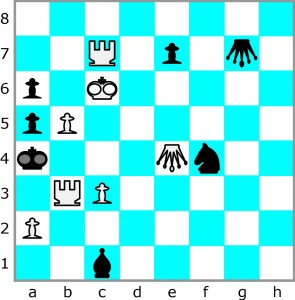
Poniżej dwuchodówka – przykład i proste ćwiczenie, ilustrujące ruchy i możliwości koników polnych. Na diagramie są dwa Kp (odwrócone hetmany). Białe zaczynają i dają mata w drugim posunięciu. W jaki sposób?

Najważniejsze i najtrudniejsze jest znalezienie ruchu kluczowego, czyli pierwszego białych, zapewniającego wygraną niezależnie od odpowiedzi czarnych. Ruchem tym jest 1. Kc6-b7. Po nim grozi mat 2. Wc7-c4. Skok 1. … Kpg7-d7+ nie zapobiega tej groźbie (mimo szacha), bo mat wieżą jest równocześnie obroną przed szachem. Wszystkie pozostałe możliwości obrony, od A do E,  podane są poniżej. Proszę wpisać pod każdą – w miejsce znaku zapytania – drugi, czyli matujący ruch białych.
A. 1. …  Kpg7-b2
    2. ?
B. 1. …  Gc1-a3
    2. ?
C. 1. …  a6xb5
    2. ?
D. 1. …  Sf4-d5
    2. ?
E. 1. …  Sf4-d3
    2. ?
W następnym wpisie zaproszę chętnych do samodzielnego ujeżdżania konika. Będzie konkurs z nagrodą.